Coordenadas generalizadas (CMR)

De Laplace

Revisión a fecha de 10:09 10 ene 2017; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Definición
3 Ecuaciones de vínculo
- 3.1 Vínculos geométricos
- 3.2 Vínculos cinemáticos
4 Principio de D'Alembert

1 Introducción

hemos visto que el principio de D'Alembert, tal como lo hemos formulado, es poco útil como herramienta incluso en casos sencillos como el del péndulo. La razón está en que se ha enunciado en términos de las coordenadas cartesianas de las partículas. Estas coordenadas son adecuadas si en el sistema solo aparecen rectas y planos, pero no son las preferibles en el caso de que haya superficies curvas.

No obstante, el principio puede generalizarse a otras coordenadas, como pueden ser las cilíndricas o esféricas o cuales quiera otras que nos interesen en un problema concreto. De hecho, la gran ventaja del principio de D'Alembert es que, al tratarse de una expresión escalar puede ser generalizado a toda clase de coordenadas sin tener que preocuparnos mucho de la elección de sistemas de referencia, ejes o bases vectoriales.

2 Definición

Para llegar a esta expresión general, suponemos que las coordenadas cartesianas puedene escribirse como funciones d eun conjunto de coordenadas generalizadas

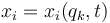
$x_i= x_i(q_k,t)\,$

La condición que deben cumplir las coordenadas generalizadas es que definan de forma unívoca el estado del sistema. Por ello, el conjunto de las $q k$ debe ser al menos de tantas coordenadas como grados de libertad tenga el sistema.

Las coordenadas generalizadas identifican el estado del sistema como un punto en el espacio de las $q k$ . A este espacio abstracto se lo denomina espacio de configuración.

Hallando la diferencial de las coordenadas cartesianas obtenemos

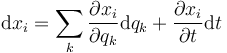
$\mathrm{d}x_i=\sum_k \frac{\partial x_i}{\partial q_k}\mathrm{d}q_k+\frac{\partial x_i}{\partial t}\mathrm{d}t$

lo que nos da la relación entre los desplazamientos virtuales

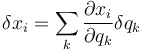
$\delta x_i=\sum_k \frac{\partial x_i}{\partial q_k}\delta q_k$

y también entre velocidades

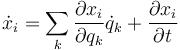
$\dot{x}_i=\sum_k \frac{\partial x_i}{\partial q_k}\dot{q}_k+\frac{\partial x_i}{\partial t}$

Vemos que 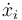$\dot{x}_i$ depende tanto de las coordenadas generalizadas, 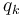$q_k\,$ como de las velocidades generalizadas, 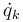$\dot{q}_k$ , cumpliéndose la relación

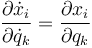
$\frac{\partial \dot{x}_i}{\partial \dot{q}_k}=\frac{\partial x_i}{\partial q_k}$

3 Ecuaciones de vínculo

3.1 Vínculos geométricos

Los vínculos entre coordenadas cartesianas pueden convertirse en relaciones entre coordenadas generalizadas por simple sustitución

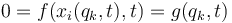
$0=f(x_i(q_k,t),t) = g(q_k,t)\,$

El péndulo simple

Si efectuamos el cambio a polares

$x = \rho\cos(\theta)\qquad \qquad y = \rho\,\mathrm{sen}(\theta)$

el vínculo

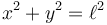
$x^2 +y^2 = \ell^2$

se transforma en

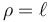
$\rho = \ell\,$

mientras que sobre $θ$ no hay vínculo alguno.

3.2 Vínculos cinemáticos

Si las coordenadas cartesianas verifican relaciones de vínculo del tipo

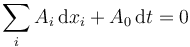
$\sum_i A_{i}\,\mathrm{d}x_i+A_{0}\,\mathrm{d}t=0$

o equivalentemente

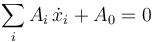
$\sum_i A_{i}\,\dot{x}_i+A_{0}=0$

estas relaciones se pueden transformar en vínculos sobre las coordenadas generalizadas por sustitución

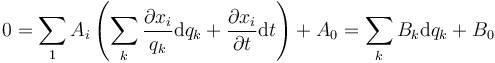
$0=\sum_1 A_i\left(\sum_k \frac{\partial x_i}{q_k}\mathrm{d}q_k+\frac{\partial x_i}{\partial t}\mathrm{d}t\right)+A_0=\sum_k B_k \mathrm{d}q_k+B_0$

o

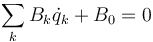
$\sum_k B_k\dot{q}_k+B_0=0$

donde

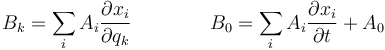
$B_k=\sum_i A_i \frac{\partial x_i}{\partial q_k}\qquad\qquad B_0=\sum_i A_i\frac{\partial x_i}{\partial t}+A_0$

con las coordenadas cartesianas que aparecen en los $A i$ puestas en función de las coordenadas generalizadas.

En la medida de lo posible, la elección de las nuevas coordenadas debe hacerse de manera que estas ecuaciones de vínculo sean más simples que con las coordenadas cartesianas.

El péndulo simple

En forma cinemática, el vínculo sobre la longitud del péndulo se escribe

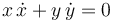
$x\,\dot{x}+y\,\dot{y}=0$

Si pasamos a polares (abreviando 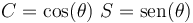$C=\cos(\theta)\ S=\mathrm{sen}(\theta)$ )

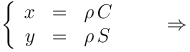
$\left\{\begin{array}{rcl}x & = & \rho\,C\\ y & = &\rho\,S\end{array}\right.\qquad\Rightarrow\qquad$

con lo que el vínculo queda

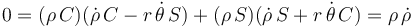
$0=(\rho\,C)(\dot{\rho} \,C-r\,\dot{\theta}\,S)+(\rho\,S)(\dot{\rho}\,S+r\,\dot{\theta}\,C)=\rho\,\dot{\rho}$

o simplificando

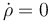
$\dot{\rho}=0$

Sobre el ángulo, como antes, no aparece vínculo alguno.

4 Principio de D'Alembert

Si llevamos la relación entre desplazamientos virtuales al principio de D'Alembert nos queda

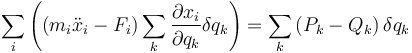
$\sum_i\left((m_i\ddot{x}_i-F_i)\sum_k \frac{\partial x_i}{\partial q_k}\delta q_k\right) = \sum_k\left(P_k-Q_k\right)\delta q_k$

donde

$P_k = \sum_i m_i \ddot{x}_i\frac{\partial x_i}{\partial q_k} \qquad\qquad Q_k = \sum_i F_i\frac{\partial x_i}{\partial q_k}$

A la cantidad $Q k$ se la conoce como fuerza generalizada. La cantidad $P k$ no tiene nombre específico, pero por analogía podemos decir que $- P k$ es una fuerza de inercia generalizada.

Coordenadas generalizadas (CMR)

De Laplace

Contenido

1 Introducción

2 Definición

3 Ecuaciones de vínculo

3.1 Vínculos geométricos

3.2 Vínculos cinemáticos

4 Principio de D'Alembert

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES