Coordenadas generalizadas (CMR)

De Laplace

Contenido

1 Introducción
2 Definición
3 Ecuaciones de vínculo
- 3.1 Vínculos geométricos
- 3.2 Vínculos cinemáticos
4 Principio de D'Alembert
- 4.1 Casos holónomos
- 4.2 Casos no holónomos
5 Sólidos rígidos

1 Introducción

Hemos visto que el principio de D'Alembert, tal como lo hemos formulado, es poco útil como herramienta incluso en casos sencillos como el del péndulo. La razón está en que se ha enunciado en términos de las coordenadas cartesianas de las partículas. Estas coordenadas son adecuadas si en el sistema solo aparecen rectas y planos, pero no son las preferibles en el caso de que haya superficies curvas.

No obstante, el principio puede generalizarse a otras coordenadas, como pueden ser las cilíndricas o esféricas o cuales quiera otras que nos interesen en un problema concreto. De hecho, la gran ventaja del principio de D'Alembert es que, al tratarse de una expresión escalar puede ser generalizado a toda clase de coordenadas sin tener que preocuparnos mucho de la elección de sistemas de referencia, ejes o bases vectoriales.

2 Definición

Para llegar a esta expresión general, suponemos que las coordenadas cartesianas puedene escribirse como funciones de un conjunto de coordenadas generalizadas

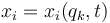
$x_i= x_i(q_k,t)\,$

La condición que deben cumplir las coordenadas generalizadas es que definan de forma unívoca el estado del sistema. Por ello, el conjunto de las $q k$ debe ser al menos de tantas coordenadas como grados de libertad tenga el sistema.

Las coordenadas generalizadas identifican el estado del sistema como un punto en el espacio de las $q k$ . A este espacio abstracto se lo denomina espacio de configuración.

Hallando la diferencial de las coordenadas cartesianas obtenemos

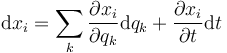
$\mathrm{d}x_i=\sum_k \frac{\partial x_i}{\partial q_k}\mathrm{d}q_k+\frac{\partial x_i}{\partial t}\mathrm{d}t$

lo que nos da la relación entre los desplazamientos virtuales

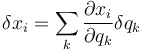
$\delta x_i=\sum_k \frac{\partial x_i}{\partial q_k}\delta q_k$

y también entre velocidades

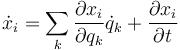
$\dot{x}_i=\sum_k \frac{\partial x_i}{\partial q_k}\dot{q}_k+\frac{\partial x_i}{\partial t}$

Vemos que 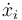$\dot{x}_i$ depende tanto de las coordenadas generalizadas, 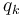$q_k\,$ como de las velocidades generalizadas, 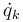$\dot{q}_k$ , cumpliéndose la relación

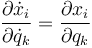
$\frac{\partial \dot{x}_i}{\partial \dot{q}_k}=\frac{\partial x_i}{\partial q_k}$

3 Ecuaciones de vínculo

3.1 Vínculos geométricos

Los vínculos entre coordenadas cartesianas pueden convertirse en relaciones entre coordenadas generalizadas por simple sustitución

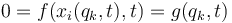
$0=f(x_i(q_k,t),t) = g(q_k,t)\,$

El péndulo simple

Si efectuamos el cambio a polares

$x = \rho\cos(\theta)\qquad \qquad y = \rho\,\mathrm{sen}(\theta)$

el vínculo

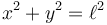
$x^2 +y^2 = \ell^2$

se transforma en

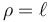
$\rho = \ell\,$

mientras que sobre $θ$ no hay vínculo alguno.

3.2 Vínculos cinemáticos

Si las coordenadas cartesianas verifican relaciones de vínculo del tipo

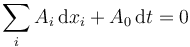
$\sum_i A_{i}\,\mathrm{d}x_i+A_{0}\,\mathrm{d}t=0$

o equivalentemente

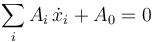
$\sum_i A_{i}\,\dot{x}_i+A_{0}=0$

estas relaciones se pueden transformar en vínculos sobre las coordenadas generalizadas por sustitución

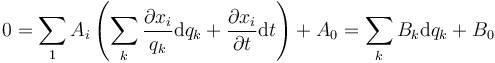
$0=\sum_1 A_i\left(\sum_k \frac{\partial x_i}{q_k}\mathrm{d}q_k+\frac{\partial x_i}{\partial t}\mathrm{d}t\right)+A_0=\sum_k B_k \mathrm{d}q_k+B_0$

o

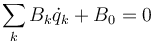
$\sum_k B_k\dot{q}_k+B_0=0\,$

donde

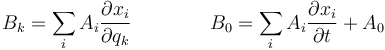
$B_k=\sum_i A_i \frac{\partial x_i}{\partial q_k}\qquad\qquad B_0=\sum_i A_i\frac{\partial x_i}{\partial t}+A_0$

con las coordenadas cartesianas que aparecen en los $A i$ puestas en función de las coordenadas generalizadas.

La relación correspondiente para desplazamientos virtuales será

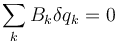
$\sum_k B_k\delta q_k=0\,$

En la medida de lo posible, la elección de las nuevas coordenadas debe hacerse de manera que estas ecuaciones de vínculo sean más simples que con las coordenadas cartesianas.

El péndulo simple

En forma cinemática, el vínculo sobre la longitud del péndulo se escribe

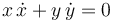
$x\,\dot{x}+y\,\dot{y}=0$

Si pasamos a polares (abreviando 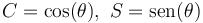$C=\cos(\theta),\ S=\mathrm{sen}(\theta)$ )

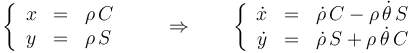
$\left\{\begin{array}{rcl}x & = & \rho\,C\\ y & = &\rho\,S\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\dot{x} & = & \dot{\rho} \,C-\rho\,\dot{\theta}\,S\\ \dot{y} & = &\dot{\rho}\,S+\rho\,\dot{\theta}\,C\end{array}\right.$

con lo que el vínculo queda

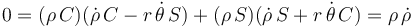
$0=(\rho\,C)(\dot{\rho} \,C-r\,\dot{\theta}\,S)+(\rho\,S)(\dot{\rho}\,S+r\,\dot{\theta}\,C)=\rho\,\dot{\rho}$

o simplificando

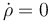
$\dot{\rho}=0$

Sobre el ángulo, como antes, no aparece vínculo alguno.

4 Principio de D'Alembert

Si llevamos la relación entre desplazamientos virtuales al principio de D'Alembert nos queda

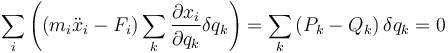
$\sum_i\left((m_i\ddot{x}_i-F_i)\sum_k \frac{\partial x_i}{\partial q_k}\delta q_k\right) = \sum_k\left(P_k-Q_k\right)\delta q_k=0$

donde

$P_k = \sum_i m_i \ddot{x}_i\frac{\partial x_i}{\partial q_k} \qquad\qquad Q_k = \sum_i F_i\frac{\partial x_i}{\partial q_k}$

A la cantidad $Q k$ se la conoce como fuerza generalizada. La cantidad $P k$ no tiene nombre específico, pero por analogía podemos decir que $- P k$ es una fuerza de inercia generalizada.

Las fuerzas generalizadas no son fuerzas en general (en el sentido de que no se miden en newtons). Si la variable $q k$ es un ángulo, la fuerza generalizada representa el momento de las fuerzas que producen un giro alrededor de ese eje de rotación.

Las fuerzas generalizadas de reacción vincular se calculan, como en el caso cartesiano, mediante los multiplicadore de Lagrange

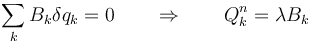
$\sum_k B_k\delta q_k=0\qquad\Rightarrow\qquad Q^n_k=\lambda B_k$

Llegados a este punto, podemos operar con el principio de D'Alembert en función de las coordenadas generalizadas tal y como hicimos con las cartesianas: identificando diferenciales independientes y anulando los coeficientes respectivos.

4.1 Casos holónomos

Cuando todos los vínculos son geométricos o, siendo cinemáticos, son integrables (es decir, cuando son holónomos), podemos, en teoría, definir un número mínimo de coordenadas generalizadas, tantas como grados de libertad del sistema, de manera que los vínculos se satisfagan automáticamente. De esta forma cada uno los diferenciales es independiente y los respectivos coeficientes deben anularse por separado.

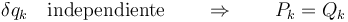
$\delta q_k\quad\mbox{independiente} \qquad\Rightarrow\qquad P_k = Q_k$

En el caso óptimo, el sistema se reduce a 3N-r ecuaciones de movimiento, en cada una de las cuales aparece una sola de las aceleraciones generalizadas, como función de las posiciones y velocidades.

Péndulo simple

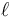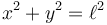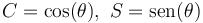En el caso de un péndulo de longitud $\ell$ que se mueve en un plano vertical tenemos un vínculo geométrico $x^2+y^2 =\ell^2$ , que reduce el número de grados de libertad a 1. Podemos reducir las ecuaciones a una sola variable (abreviando $C=\cos(\theta),\ S=\mathrm{sen}(\theta)$ )

$\left\{\begin{array}{rcl}x & = & \ell\,C\\ y & = &\ell\,S\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\delta x & = & -\ell\,S\,\delta\theta\\ \delta y & = &\ell\,C\,\delta\theta\end{array}\right.$

y por otro lado

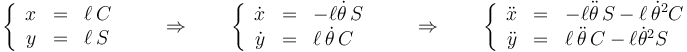
$\left\{\begin{array}{rcl}x & = & \ell\,C\\ y & = &\ell\,S\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\dot{x} & = & -\ell\dot{\theta}\,S\\ \dot{y} & = &\ell\,\dot{\theta}\,C\end{array}\right. \qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\ddot{x} & = & -\ell\ddot{\theta}\,S-\ell\,\dot{\theta}^2C\\ \ddot{y} & = &\ell\,\ddot{\theta}\,C-\ell\dot{\theta}^2S\end{array}\right.$

Llevando esto a la ecuación fundamental de la dinámica (tomando el eje X vertical y hacia abajo)

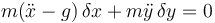
$m(\ddot{x}-g)\,\delta x + m\ddot{y}\,\delta y =0$

resulta

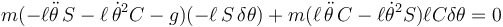
$m(-\ell\ddot{\theta}\,S-\ell\,\dot{\theta}^2C-g)(-\ell\,S\,\delta\theta)+m(\ell\,\ddot{\theta}\,C-\ell\dot{\theta}^2S)\ell C\delta\theta = 0$

que se simplifica a

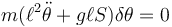
$m(\ell^2\ddot{\theta}+g\ell S)\delta\theta=0$

es decir

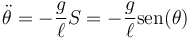
$\ddot{\theta}=-\frac{g}{\ell}S=-\frac{g}{\ell}\mathrm{sen}(\theta)$

4.2 Casos no holónomos

En los casos de vínculos cinemáticos no integrables, no es posible elegir un sistema de coordenadas tal que todos los vínculos se satisfagan automáticamente. Por ello, para describir el sistema son precisas más coordenadas generalizadas que grados de libertad tiene.

Cuando hay vínculos no holónomos es necesario usar el principio de D'Alembert completo y no dar por supuesto que cada coeficiente es independiente. A partir de los vínculos se establecen relaciones entre los desplazamientos virtuales que permiten identificar que desplazamientos son independientes.

El problema del patín

Un caso de vínculo no holónomo lo da la presencia de un patín sobre hielo, que podemos modelar como que la velocidad en el punto de contacto es siempre paralela a la cuchilla.

Si tenemos sobre un plano dos masas iguales unidas por una varilla ideal sin masa, y una de ellas (la 1) está sobre una cuchilla alineada con la varilla tenemos dos vínculos:

Uno holónomo, ya que la distancia entre las partículas está fijada

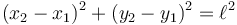
$(x_2-x_1)^2+(y_2-y_1)^2 = \ell^2$

Uno no holónomo, que consiste en que la velocidad de la partícula 1 va alineada con la varilla

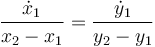
$\frac{\dot{x}_1}{x_2-x_1}=\frac{\dot{y}_1}{y_2-y_1}$

El primero de los dos lo podemos eliminar eligiendo como coordenadas generalizadas la posición de la masa 1 y el ángulo que la varilla forma con el eje OX. De esta manera

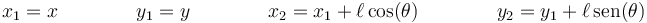
$x_1=x\qquad\qquad y_1 = y\qquad\qquad x_2=x_1+\ell\cos(\theta)\qquad\qquad y_2=y_1+\ell\,\mathrm{sen}(\theta)$

y el vínculo no holónomo queda en la forma

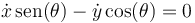
$\dot{x}\,\mathrm{sen}(\theta)-\dot{y}\cos(\theta)=0$

o, en foma pfaffiana para los desplazamientos virtuales

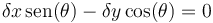
$\delta x\,\mathrm{sen}(\theta)-\delta y\cos(\theta)=0$

Esta expresión permite reducir las ecuaciones de movimiento a dos, en función de tres coordenadas, relacionadas entre sí mediante la ecuación del vínculo.

5 Sólidos rígidos

El caso de un sólido rígido es especial, no solo por su importancia práctica, sino porque muestra cómo puede reducirse un sistema de miles de milllones de coordenadas (tres por partícula) a solo seis (en el caso tridimensional) o solo tres (en el caso plano)

La condición de rigidez implica que la velocidad de cada punto del sólido cumple

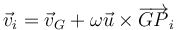
$\vec{v}_i =\vec{v}_G+\omega\vec{u}\times\overrightarrow{GP}_i$

siendo $\vec{u}$ en la dirección del eje instantáneo de rotación y por tanto del vecyor velocidad angular.

Si multiplicamos por el diferencial de tiempo

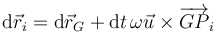
$\mathrm{d}\vec{r}_i=\mathrm{d}\vec{r}_G+\mathrm{d}t\,\omega\vec{u}\times\overrightarrow{GP}_i$

El producto 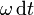$\omega\,\mathrm{d}t$ es igual al diferencial del ángulo girado, $dθ$ alrededor del eje instantáneo de rotación. La relación resultante es catastática, por lo que se pueden sustituir los desplazamientos posibles por desplazamientos virtuales

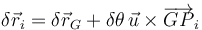
$\delta\vec{r}_i=\delta\vec{r}_G+\delta\theta\,\vec{u}\times \overrightarrow{GP}_i$

Llevamos estas relaciones al principio de D'Alembert

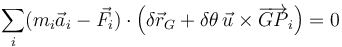
$\sum_i (m_i\vec{a}_i-\vec{F}_i)\cdot\left(\delta\vec{r}_G+\delta\theta\,\vec{u}\times \overrightarrow{GP}_i\right)=0$

En este sumatorio podemos extraer los factores comunes a todos los términos

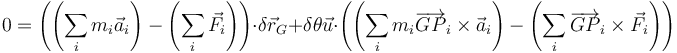
$0=\left(\left(\sum_im_i\vec{a}_i\right)-\left(\sum_i\vec{F}_i\right)\right)\cdot\delta\vec{r}_G+\delta\theta\vec{u}\cdot\left(\left(\sum_i m_i\overrightarrow{GP}_i\times\vec{a}_i\right)-\left(\sum_i\overrightarrow{GP}_i\times\vec{F}_i\right)\right)$

Podemos identificar cada uno de los cuatro términos y escribir la expresión como

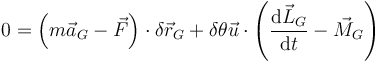
$0 = \left(m\vec{a}_G-\vec{F}\right)\cdot\delta\vec{r}_G+\delta\theta\vec{u}\cdot\left(\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}-\vec{M}_G\right)$

es decir, el principio de D'Alembert para un sólido se reduce a estudiar la evolución del centro de masas y el momento cinético alrededor del centro de masas.

En el caso de un sólido no vinculado, las tres coordenadas del CM varían libremente y también lo hacen las tres componentes de la velocidad angular, por lo que se anulan por separado los dos coeficientes, resultando las conocidas ecuaciones de la dinámica del sólido.

$m\vec{a}_G=\vec{F}\qquad\qquad \frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}=\vec{M}_G$

Si el sólido describe un movimiento plano, la dirección del eje de rotación está fijada, y el desplazamiento debe ser bidimensional. Si estos tres grados de libertad son independientes, resultan las ecuaciones

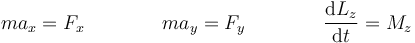
$ma_x = F_x\qquad\qquad m a_y = F_y\qquad\qquad \frac{\mathrm{d}L_z}{\mathrm{d}t}=M_z$

Pudiera ser que haya fuerzas aplicadas en la dirección vertical o pares aplicados en la dirección X o Y, pero se ven compensados por fuerzas o momentos de reacción. Para determinar estos habría que desvincular el sólido.

Si se trata de un sólido que gira alrededor de un eje fijo, la dirección de $\vec{u}$ está fijada. Además el centro de masas describirá circunferencias en torno al eje fijo

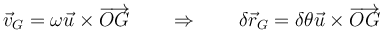
$\vec{v}_G=\omega\vec{u}\times \overrightarrow{OG}\qquad\Rightarrow\qquad \delta\vec{r}_G = \delta\theta\vec{u}\times\overrightarrow{OG}$

y el principio de D'Alembert se reduce a

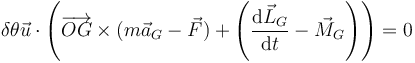
$\delta\theta\vec{u}\cdot\left(\overrightarrow{OG}\times(m\vec{a}_G-\vec{F})+\left(\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}-\vec{M}_G\right)\right)=0$

Si la rotación es libre el coeficiente debe anularse y la ecuación se reduce a (usando las fórmulas del cambio de centro de reducción)

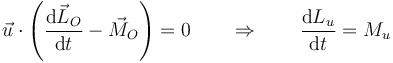
$\vec{u}\cdot\left(\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}-\vec{M}_O\right)=0\qquad\Rightarrow\qquad \frac{\mathrm{d}L_u}{\mathrm{d}t}=M_u$

que nos dice que el estudio de esta rotación se reduce a determinar cómo varía la componente del momento cinético paralela al eje de rotación por efecto del par de las fuerzas externas aplicadas. Para el resto de componentes no obtenemos ecuaciones, pero desvinculando pueden determinarse las fuerzas y pares de reacción.

Coordenadas generalizadas (CMR)

De Laplace

Contenido

1 Introducción

2 Definición

3 Ecuaciones de vínculo

3.1 Vínculos geométricos

3.2 Vínculos cinemáticos

4 Principio de D'Alembert

4.1 Casos holónomos

4.2 Casos no holónomos

5 Sólidos rígidos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES