Tercera Convocatoria Ordinaria 2016/17 (MR G.I.C.)
De Laplace
Revisión a fecha de 16:24 9 dic 2016; Pedro (Discusión | contribuciones)
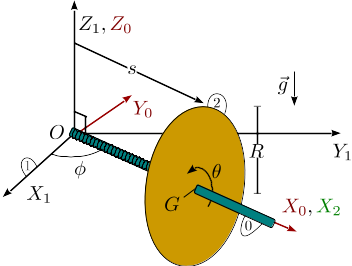
Disco deslizando por barra horizontal con muelle
El disco plano de la figura, (sólido "2", masa m, radio R) desliza sin
rozamiento
sobre una barra rígida (sólido "0") de masa despreciable, a la vez que
rota alrededor de ella. A su vez esta barra, que permanece siempre en el plano OX1Y1,
rota alrededor el eje OZ0. Un muelle de constante elástica k y longitud
natural R conecta el punto O con el centro del disco. En el instante inicial
se tiene s(0) = 2R,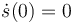 
, φ(0) = 0, 
,
.
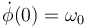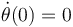- Determina la reducción cinemática del centro de masas del sólido "2" (punto G) en su movimiento absoluto, así como su derivada temporal.
- Encuentra la expresión de la energía cinética del disco, así como su momento cinético respecto a O.
- Haz la desvinculación global del disco en su centro de masas. Indica cuantas incógnitas hay en el problema y que ecuaciones usarías para resolverlo (no hace falta escribir las ecuaciones)
- Encuentra y escribe dos integrales primeras del movimiento.
