De Laplace

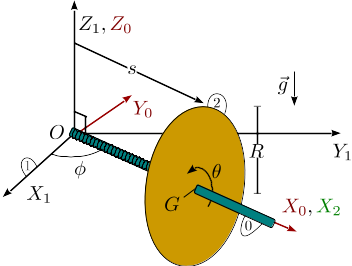
1 Disco deslizando por barra horizontal con muelle

El disco plano de la figura, (sólido "2", masa $m$ , radio $R$ ) desliza sin rozamiento sobre una barra rígida (sólido "0") de masa despreciable, a la vez que rota alrededor de ella. A su vez esta barra, que permanece siempre en el plano $O X 1 Y 1$ , rota alrededor el eje $O Z 0$ . Un muelle de constante elástica $k$ y longitud natural $R$ conecta el punto $O$ con el centro del disco. 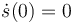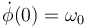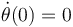En el instante inicial se tiene $s (0) = 2 R$ , $\dot{s}(0)=0$ , $φ(0) = 0$ , $\dot{\phi}(0)=\omega_0$ , $\dot{\theta}(0)=0$ .

Determina la reducción cinemática del centro de masas del sólido "2" (punto $G$ ) en su movimiento absoluto, así como su derivada temporal.
Encuentra la expresión de la energía cinética del disco, así como su momento cinético respecto a $O$ .
Haz la desvinculación global del disco en su centro de masas. Indica cuantas incógnitas hay en el problema y que ecuaciones usarías para resolverlo (no hace falta escribir las ecuaciones)
Encuentra y escribe dos integrales primeras del movimiento.

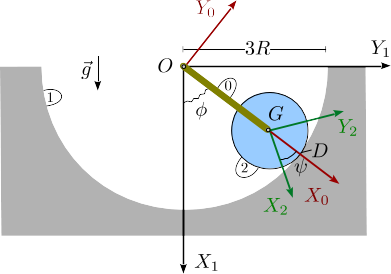
2 Disco rodando en cavidad con muelle de torsión

Un disco de radio $R$ y masa $m$ (sólido "2") rueda sin deslizar sobre una superficie circular cóncava (sólido "1") de radio $3 R$ . En el centro del disco se articula una barra (sólido "0") de masa despreciable y longitud $2 R$ . El otro extremo de la barra se articula en un punto fijo $O$ . La barra está conectada a su vez a un resorte de torsión en el punto $O$ . Este resorte ejerce un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él se puede expresar como $U k = k φ 2$ , siendo $k$ una constante.

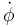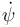Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre $\dot{\phi}$ y $\dot{\psi}$ ?.
Calcula la energía cinética del disco y su energía potencial.
Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo $φ$ es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación.
Estando el disco en reposo y con $φ = 0$ , se aplica al centro del disco una percusión 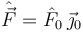$\hat{\vec{F}} = \hat{F}_0\,\vec{\jmath}_0$ . Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje. $O Y 1$ .