Sistemas equivalentes de fuerzas (CMR)

De Laplace

Revisión a fecha de 21:22 8 dic 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Sistemas equivalentes

De las ecuaciones anteriores

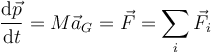
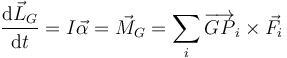
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=M\vec{a}_G=\vec{F}=\sum_i\vec{F}_i$ $\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}=I\vec{\alpha}=\vec{M}_G=\sum_i\overrightarrow{GP}_i\times\vec{F}_i$

se deduce que para determinar la evolución de un sólido solo precisamos dos cantidades vectoriales:

La resultante $\vec{F}$ , suma vectorial de las fuerzas externas aplicadas sobre el sólido
El momento resultante $\vec{M}_G$ , suma vectorial de los momentos de las fuerzas aplicadas respecto al CM del sólido.

Aunque la expresión de las ecuaciones de movimiento quedan más simples si se emplea como punto de referencia (“centro de reducción”) el centro de masas, puede emplear un punto fijo arbitrario A, siendo la ecuación correspondiente

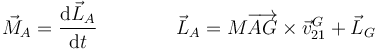
$\vec{M}_A = \frac{\mathrm{d}\vec{L}_A}{\mathrm{d}t}\qquad\qquad \vec{L}_A=M\overrightarrow{AG}\times\vec{v}_{21}^G+\vec{L}_G$

y dado el momento de las fuerzas hallado respecto a un punto podemos hallar el correspondiente a cualquier otro con la relación

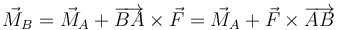
$\vec{M}_B = \vec{M}_A + \overrightarrow{BA}\times\vec{F}=\vec{M}_A + \vec{F}\times \overrightarrow{AB}$

Esto quiere decir que los diferentes sistemas de fuerzas que actúan sobre un sólido pueden clasificarse en sistemas equivalentes, identificados cada uno por la fuerza resultante y el momento resultante. Dos sistemas equivalentes tendrán el mismo efecto físico sobre el sólido.

Por ejemplo, dado un bloque situado sobre un suelo horizontal, no existe diferencia física entre empujarlo horizontalmente por su parte trasera o tirar horizontalmente desde la delantera. En ambos casos, la resultante es la misma y también lo es el momento de las fuerzas.

Por ello, el análisis de los casos posibles puede reducirse a los casos más sencillos. Dada la similitud entre la relación entre momentos y el teorema de Chasles, la lista de casos posibles es análoga a la clasificación de los movimientos rígidos.

1.1 Vectores deslizantes

Se denomina recta soporte de una fuerza $\vec{F}_0$ aplicada en un punto $P 0$ a aquella que pasa por el punto de aplicación y lleva la dirección de la fuerza:

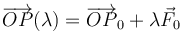
$\overrightarrow{OP}(\lambda)=\overrightarrow{OP}_0+\lambda\vec{F}_0$

Por las propiedades del producto vectorial, el momento de la fuerza $\vec{F}_0$ es el mismo si en vez de estar aplicada en $P 0$ está aplicada en cualquier otro punto $P 1$ de la recta soporte.

$\vec{M}_O=\overrightarrow{OP}_1\times\vec{F}_0=\left(\overrightarrow{OP}_0+\lambda\vec{F}_0\right)\times\vec{F}_0=\overrightarrow{OP}_0\times\vec{F}_0$

Por ello, se dice que las fuerzas aplicadas sobre un sólido son vectores deslizantes. El efecto físico que producen es el mismo si se desliza su punto de aplicación a lo largo de la recta soporte.

1.2 Teorema de Varignon

De entre los diferentes teoremas aplicables para la determinación de sistemas equivalenteso, existe uno de especial utilidad, especialmente en el caso de figuras planas, ya que facilita la solución por métodos geométricos.

Dadas varias fuerzas concurrentes el momento resultante de las distintas fuerzas es igual al momento de la resultante de ellas aplicada en el punto de concurrencia.

Donde entendemos como fuerzas concurrentes aquellas cuyas rectas soporte se cortan en un punto P.

La demostración es la siguiente: tenemos $n$ fuerzas concurrentes, 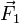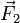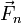$\vec{F}_1$ , $\vec{F}_2$ ,... $\vec{F}_n$ , aplicadas en los puntos $A 1$ , $A 2$ ,... $A n$ . El momento resultante respecto a un punto O es

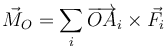
$\vec{M}_O=\sum_i \overrightarrow{OA}_i\times\vec{F}_i$

Ahora bien, por pasar cada recta soporte por el punto de concurrencia P se cumple para cada una

$\overrightarrow{PA}_i\times\vec{F}_i=\vec{0}$

por ser vectores paralelos. Por tanto, para cada momento individual

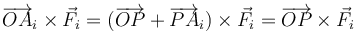
$\overrightarrow{OA}_i\times\vec{F}_i = (\overrightarrow{OP}+\overrightarrow{PA}_i)\times\vec{F}_i=\overrightarrow{OP}\times\vec{F}_i$

y para la resultante

$\vec{M}_O=\sum_i \overrightarrow{OP}\times\vec{F}_i=\overrightarrow{OP}\times\left(\sum_i\vec{F}_i\right)=\overrightarrow{OP}\times\vec{F}$

Por tanto, el procedimiento para hallar el momento resultante consiste en llevar todas las fuerzas al punto de concurrencia, hallar la resultante de todas las fuerzas y luego calcular su momento respecto al punto O.

Empleando las propiedades de los vectores deslizantes, el teorema de Varignon, y otras propiedades de los sistemas de fuerzas, es posible ir reduciendo un sistema a uno equivalente formado por solo dos fuerzas o, lo que es lo mismo, una fuerza y un momento, que determinan completamente la dinámica del sólido.

Sistemas equivalentes de fuerzas (CMR)

De Laplace

1 Sistemas equivalentes

1.1 Vectores deslizantes

1.2 Teorema de Varignon

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES