Dos discos articulados en un eje
De Laplace
Revisión a fecha de 14:18 27 nov 2016; Antonio (Discusión | contribuciones)
1 Enunciado
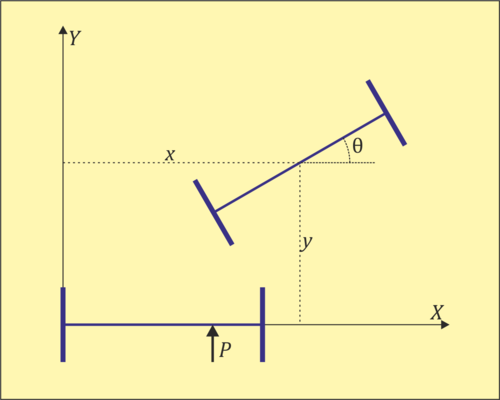
Dos discos delgados, ambos de masa m y radio r, están conectados por un eje delgado de masa m0 y longitud b. Los discos pueden rodar sin deslizar por el plano OXY. El eje está articulado en dos rodamientos, de forma que las dos ruedas pueden girar libremente en torno a él.
- Determine la energía cinética del sistema en función de la velocidad del CM del conjunto y de la velocidad angular
 con la que gira la barra en torno a un eje vertical.
con la que gira la barra en torno a un eje vertical.
- Suponga que, estando en reposo el sistema con el eje alineado con el OX y el punto de contacto de uno de los discos situado en el origen se aplica una percusión
 horizontal y perpendicular a la barra a una distancia c de su centro. Determine el movimiento del sistema a partir de ese momento
horizontal y perpendicular a la barra a una distancia c de su centro. Determine el movimiento del sistema a partir de ese momento
2 Resultados
- Cantidad de movimiento
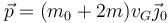
Siendo la base 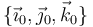 una ligada al eje, con el OX0 a lo largo de él, y el OZ0 perpendicular al plano de movimiento.
una ligada al eje, con el OX0 a lo largo de él, y el OZ0 perpendicular al plano de movimiento.
vG se relaciona con las coordenadas como
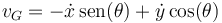
- Momento cinético respecto al CM
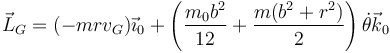
- Energía cinética
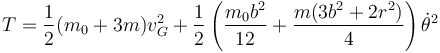
- Velocidad del CM tras la percusión
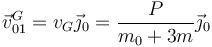
- Velocidad angular del eje tras la percusión
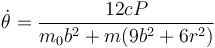
Tras la percusión, ambas cantidades permanecen constantes.





