Dinámica impulsiva vectorial (CMR)

De Laplace

Revisión a fecha de 15:10 23 nov 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Definición de percusión
2 Leyes de la dinámica impulsiva
3 Percusiones de reacción
4 Teorema de la cantidad de movimiento
5 Teorema del momento cinético
6 Teorema de la energía cinética
7 Ejemplos

1 Definición de percusión

Cuando una partícula experimenta una fuerza muy intensa (fuerza impulsiva) durante un breve intervalo de tiempo se dice que ha sufrido una percusión. Un típico ejemplo de percusión es una colisión entre una partícula y una pared.

Las percusiones se modelan mediante la hipótesis de una fuerza no nula que actúa solo durante un intervalo $Δ t$ de forma que se define la percusión debido a esta fuerza mediante la integral

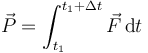
$\vec{P}=\int_{t_1}^{t_1+\Delta t}\vec{F}\,\mathrm{d}t$

La duración de la percusión se supone infinitesimal comparada con el tiempo característico de movimiento de la partícula. Esto implica que la fuerza media 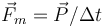$\vec{F}_m =\vec{P}/\Delta t$ es gigantesca comparada con el resto de fuerzas aplicadas. Esto permite dividir la evolución de un sistema sometido a percusiones en tres fases:

Previa a la percusión, en que la partícula actúa sometida a fuerzas aplicadas no impulsivas y su posición y velocidad evolucionan gradualmente.
Durante la percusión, puede considerarse que la partícula se mueve sometida exclusivamente a las fuerzas impulsivas, ya que el resto son despreciables. Durante este breve intervalo de tiempo puede suponerse que la velocidad de la partícula experimenta un salto finito, pero que la posición de la partícula no cambia.
Tras la percusión, la partícula vuelve a moverse sometida a fuerzas aplicadas no impulsivas, pero con unas condiciones iniciales que son el resultado de aplicar la percusión.

Normalmente para estudiar las percusiones no es preciso conocer el detalle de las fuerzas impulsivas (que pueden ser extremadamente complejas, como en el caso de una colisión de una pelota con una pared). Así, durante una colisión de un objeto aparentemente rígido se producen deformaciones elevadas que hacen inválida la hipótesis de rigidez. Si fuera necesario, se hacen modelos como suponer que la fuerza se comporta como un pulso rectangular o un pulso gaussiano, muy estrechos.

Nos interesará sobre todo el relacionar el estado tras la percusión con el estado previo a ella. Para ello emplearemos la notación de salto para indicar la variación de una magnitud. Si la percusión ocurre en $t = t 1$ denotaremos el salto de una magnitud A como su incremento

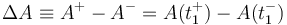
$\Delta A\equiv A^+-A^-=A(t_1^+)-A(t_1^-)$

El efecto de una percusión es entonces provocar un salto finito en la velocidad. No así en la posición, ya que el breve intervalo en que actúa se supone que no es suficiente para producir un desplazamiento apreciable. En notación de salto

$\Delta \vec{v}\neq \vec{0}\qquad\qquad \Delta \vec{r}=\vec{0}$

2 Leyes de la dinámica impulsiva

Las percusiones, como las fuerzas de las que proceden verifican las leyes de Newton.

Así, dado un sistema de partículas, podemos dividir las percusiones entre internas y externas.

Las percusiones internas satisfacen la tercera ley de Newton, de forma que si una partícula A ejerce una percusión sobre B, B ejerce sobre A una igual en magnitud y dirección y sentido opuesto

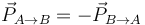
$\vec{P}_{A\to B}=-\vec{P}_{B\to A}$

y además va en la dirección de la recta que une los dos puntos, lo que implica

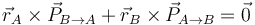
$\vec{r}_A\times\vec{P}_{B\to A}+\vec{r}_B\times\vec{P}_{A\to B}=\vec{0}$

3 Percusiones de reacción

La presencia de vínculos es causa de fuerzas impulsivas de reacción. Éstas pueden ser de varios tipos, dependiendo de si el vínculo existe antes, durante o después de la percusión.

Fuerzas debidas a un vínculo permanente, presente antes, durante y después de la percusión. Así, por ejemplo, si tenemos una masa que cuelga de una varilla rígida y golpeamos la varilla en un punto por encima de la masa, el punto de donde cuelga el péndulo responde con una reacción también impulsiva.
Fuerzas debidas a la imposición de un vínculo que existe durante y después de la percusión. Cuando se impone abruptamente una nueva ligadura, la velocidad previa de la partícula puede no cumplir esta nueva condición, por lo que se ve modificada bruscamente. Este cambio abrupto en la velocidad va asociado a una fuerza de reacción impulsiva. El ejemplo característico es el del hilo inextensible que se tensa bruscamente. Por contra, la eliminación de un vínculo (el hilo que se rompe) no conlleva fuerza impulsiva, ya que la velocidad previa sigue satisfaciendo las nuevas condiciones.
Fuerzas debidas a un vínculo que existe sólo durante la percusión. El ejemplo característico es la colisión entre dos objetos rígidos.

4 Teorema de la cantidad de movimiento

Supongamos un sistema de partículas sometidas a un conjunto de percusiones 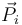$\vec{P}_i$ , que pueden ser tanto externas como internas.

Por el teorema de la cantidad de movimiento para un sistema de partículas tenemos que, en cada instante

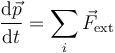
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\sum_i \vec{F}_{\mathrm{ext}}$

Si aquí integramos en el tiempo entre $t 1$ y $t 1 + Δ t$ queda

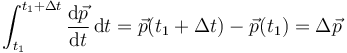
$\int_{t_1}^{t_1+\Delta t}\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\,\mathrm{d}t=\vec{p}(t_1+\Delta t)-\vec{p}(t_1)=\Delta \vec{p}$

y por tanto

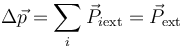
$\Delta \vec{p}=\sum_i \vec{P}_{i\mathrm{ext}}=\vec{P}_\mathrm{ext}$

Es decir, el incremento en la cantidad de movimiento del sistema es igual a la resultante de las percusiones externas aplicadas simultáneamente.

Puesto que la masa del sistema no cambia, este teorema implica un incremento en la velocidad del centro de masas:

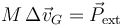
$M\,\Delta \vec{v}_G = \vec{P}_\mathrm{ext}$

5 Teorema del momento cinético

De manera similar tenemos, para el momento cinético respecto a un punto fijo o respecto al centro de masas

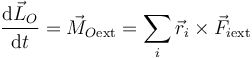
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_{O\mathrm{ext}}=\sum_i \vec{r}_i\times \vec{F}_{i\mathrm{ext}}$

Si aquñi integramos cada miembro, teniendo en cuenta que a la posición de cada partícula no le da tiempo a cambiar duante el breve periodo que dura la percusión

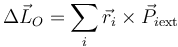
$\Delta \vec{L}_O =\sum_i \vec{r}_i\times\vec{P}_{i\mathrm{ext}}$

En el caso de que O sea el centro de masas, las posiciones serán las relativas a este punto.

Si consideramos que el centro de reducción es un punto móvil distinto del CM el teorema del momento cinético se escribe

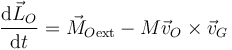
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_{O\mathrm{ext}}-M\vec{v}_O\times\vec{v}_G$

El segundo término del segundo miembro puede experimentar un salto en la percusión, pero tiene un valor finito antes, durante y después de ella. Por ello su integral sobre un intervalo muy corto tiende a 0 y que, como para el punto en reposo

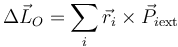
$\Delta \vec{L}_O =\sum_i \vec{r}_i\times\vec{P}_{i\mathrm{ext}}$

Si consideramos el momento cinético relativo, calculado con las velocidades respecto al centro de reducción, tenemos la ecuación de evolución

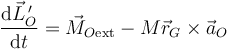
$\frac{\mathrm{d}\vec{L}^{\,\prime}_O}{\mathrm{d}t}=\vec{M}_{O\mathrm{ext}}-M\vec{r}_G\times\vec{a}_O$

En el último término la posición no cambia durante la percusión, pero la aceleración de O si puede variar, con lo que queda

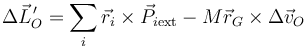
$\Delta \vec{L}^{\,\prime}_O = \sum_i \vec{r}_i\times \vec{P}_{i\mathrm{ext}}-M\vec{r}_G\times \Delta \vec{v}_O$

Si O es un punto externo al sistema cuya velocidad varía suavemente el último término se anula y recuperamos la misma fórmula que para os casos anteriores.

6 Teorema de la energía cinética

Para la energía cinética de cada partícula tenemos el incremento

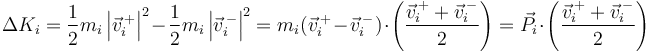
$\Delta K_i = \frac{1}{2}m_i \left|\vec{v}^{\,+}_i\right|^2-\frac{1}{2}m_i \left|\vec{v}^{\,-}_i\right|^2 = m_i(\vec{v}^{\,+}_i-\vec{v}^{\,-}_i)\cdot\left(\frac{\vec{v}^{\,+}_i+\vec{v}^{\,-}_i}{2}\right)=\vec{P}_i\cdot\left(\frac{\vec{v}^{\,+}_i+\vec{v}^{\,-}_i}{2}\right)$

es decir, lo que aumenta la energía de cada partícula es el producto de la percusión recibida por la velocidad media entre antes y después de la colisión.

Sumando para todas las partículas

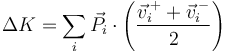
$\Delta K = \sum_i \vec{P}_i\cdot\left(\frac{\vec{v}^{\,+}_i+\vec{v}^{\,-}_i}{2}\right)$

Aquí, como en el caso de un sistema de fuerzas, es necesario incluir todas las percusiones, externas e internas.

7 Ejemplos

Dinámica impulsiva vectorial (CMR)

De Laplace

Contenido

1 Definición de percusión

2 Leyes de la dinámica impulsiva

3 Percusiones de reacción

4 Teorema de la cantidad de movimiento

5 Teorema del momento cinético

6 Teorema de la energía cinética

7 Ejemplos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES