Percusión sobre una barra (CMR)
De Laplace
Contenido |
1 Enunciado
Una masa m pende de una varilla rígida de masa despreciable y longitud b que está articulada en un punto fijo O. Se aplica una percusión horizontal en un punto de la varilla a una distancia c (c < b) de O.
- Determine la velocidad de la masa inmediatamente tras la percusión.
- Calcule el impulso de reacción en O el punto de anclaje
- Halle el incremento de la energía cinética de la masa.
- Suponga ahora que la varilla no es de masa despreciable, sino que lo que tenemos es una barra de masa M, sin masa en el extremo y articulada en O. ¿Cuánto valen en ese caso la velocidad angular de la barra tras la percusión y el impulso de reacción?
2 Velocidad de la partícula
Además de la percusión aplicada en A, aparece una percusión de reacción en el punto O, desconocida en principio. Por ello, conviene aplicar el teorema del momento cinético, tomando este punto O como centro de reducción.
De acuerdo con la versión impulsiva de este teorema
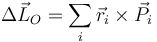
Si elegimos un sistema de ejes en que OX es horizontal y OY es vertical y hacia arriba, la percusión la aplicamos en un punto 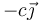 y tiene valor
y tiene valor 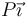 .
.
El momento cinético previo es nulo, pues la masa está en reposo.
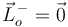
Tras la percusión, la masa adquiere una velocidad 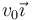 resultando en un momento cinético
resultando en un momento cinético
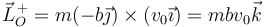
El momento impulsivo vale
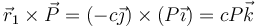
Por el teorema del momento cinético

3 Impulso de reacción
Por el teorema de la cantidad de movimiento
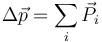
donde el sumatorio incluye tanto la percusión aplicada como la de reacción en O. Dado que conocemos la variación de la cantidad de movimiento, podemos despejar la percusión de reacción
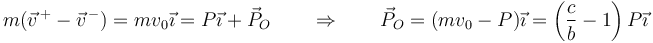
Dado que c < b esta percusión va en sentido contrario a la aplicada. Se anula si la percusión se aplica sobre la propia masa.
4 Incremento en la energía cinética
El cálculo del incremento en la energía es inmediato
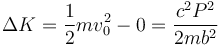
Sin embargo, parecería que este incremento no cumple la relación
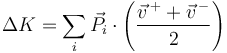
ya que si la velocidad media es cP / 2mb, el resultado no coincide con el incremento en la energía cinética (falta un factor c/b). La razón es que en el teorema de la energía cinética aparece la velocidad del punto donde se aplica la percusión, que no es la masa en este caso.
La barra efectúa un movimiento de rotación instantánea alrededor de O, con velocidad angular 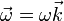 , de valor tal que
, de valor tal que
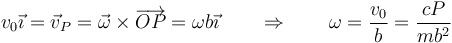
y por tanto la velocidad del punto A donde se aplica la percusión es

y, por tanto, efectivamente






