Esfera que rueda por un carril
De Laplace
Enunciado
En los experimentos de Galileo, éste hizo rodar una esfera de radio R por un carril de anchura 2b (b < R), de forma que la bola rueda apoyada en los bordes del carril, minimizando el rozamiento.
El carril se encuentra inclinado un ángulo β respecto a la horizontal.
La bola posee masa m y un momento de inercia I = γmR2 (con \gamma entre 2/5, esfera maciza y 2/5, esfera hueca).
Suponiendo que las fuerzas a ambos lados del carril son simétricas, determine la aceleración con la que la bola desciende por el carril, si inicialmente se encuentra en reposo.
Determine el ángulo β máximo para el carril si no se desea que la bola deslice.
Supóngase ahora que existe un rozamiento por rodadura de forma que en los puntos de contacto se ejerce una fuerza adicional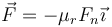 
, siendo el eje X el tangente al carril en la dirección de avance. ¿Cuál es en ese caso la aceleración de la bola?
