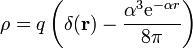Modelo de campo atómico
De Laplace
1 Enunciado
El potencial medio temporal de un átomo de hidrógeno neutro viene dado por
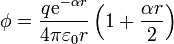
en donde q es la carga electrónica, y α − 1 = a0 / 2. Halle la distribución de carga (continua y discreta) que dará lugar a este potencial e interprete este resultado físicamente.
2 Solución
Tenemos que el potencial posee simetría de rotación, por lo que todas las derivadas e integrales van a ser sobre la coordenada esférica radial r
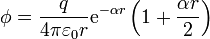
Para la densidad de carga de volumen
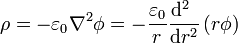
Calculamos esta derivada. Multiplicando por r
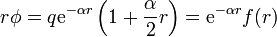
la derivada de este producto es igual a
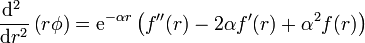
Sustituyendo f(r)
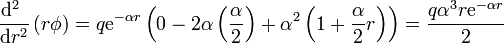
y la densidad de carga de volumen es
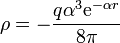
Queda la carga del núcleo, que es una carga puntual. Esta la sacamos de que el sistema es neutro, (ya que el flujo del campo eléctrico tiende a 0 para 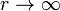 ). La carga de volumen podemos escribirla también como
). La carga de volumen podemos escribirla también como
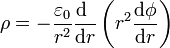
así que la carga total de volumen es
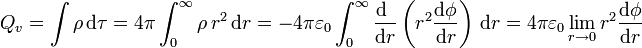
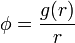
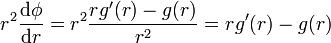
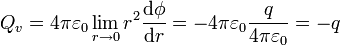
Por tanto la carga del núcleo es simplemente + q. Así pues, tenemos
- Una carga puntual + q situada en el núcleo
- Una carga − q distribuida de forma exponencial en todo el espacio
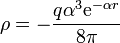
o, juntándolo todo en una sola distribución