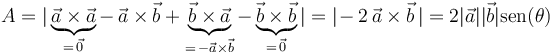No Boletín - Area de un paralelogramo (Ex.Oct/15)
De Laplace
Revisión a fecha de 02:00 7 mar 2016; Enrique (Discusión | contribuciones)
1 Enunciado
Si 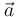 y
y 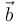 son dos vectores libres que forman un ángulo
son dos vectores libres que forman un ángulo  (siendo
(siendo 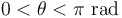 ), ¿cuánto vale el área del paralelogramo que tiene por lados a los vectores
), ¿cuánto vale el área del paralelogramo que tiene por lados a los vectores 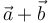 y
y 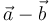 ?
?
2 Solución
Una de las propiedades geométricas estudiadas del producto vectorial permite afirmar que el área  del paralelogramo que tiene por lados a los vectores
del paralelogramo que tiene por lados a los vectores 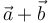 y
y 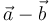 es igual a:
es igual a:
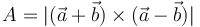
Y aplicando la propiedad distributiva del producto vectorial respecto a la suma, queda: