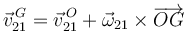Barra articulada sobre muelle Enero 2015 (MR G.I.C.)
De Laplace
Contenido |
1 Enunciado
En el sistema de la figura, la barra delgada homogénea OA (sólido "2"), de masa m y longitud L, está articulada en el punto O. El punto O puede moverse sobre el eje fijo O1Z1, y está conectado a un muelle de constante elástica k y longitud natural L. El muelle siempre permanece vertical. La barra "2" está siempre contenida en el plano O1X0Z0, como se indica en la figura.
- Encuentra la reducción cinemática del movimiento {21} en los puntos O y G.
- Calcula el momento cinético de la barra "2" en O y G (
 ,
, 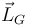 ).
).
- Calcula la energía cinética de la barra "2".
- Aplicando el T.C.M. y el T.M.C. escribe las ecuaciones de movimiento del sistema.
- Escribe todas las integrales primeras del movimiento que puedas encontrar.
2 Solución
2.1 Reducción cinemática
2.1.1 Movimiento {01}
El punto O1 pertenece al sólido "0" y está siempre en reposo respecto al sólido "1". Por tanto
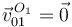
Para el vector rotación tenemos
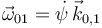
2.1.2 Movimiento {20}
De este movimiento realmente sólo nos interesa su vector rotación. El movimiento {20}
es un movimiento plano, pues el plano OX2Z2 coincide siempre con el plano O1X0Z0. El eje de rotación es perpendicular a este plano, es decir, paralelo al eje  . El eje X2 forma el ángulo φ con el eje X0, por tanto en el vector
. El eje X2 forma el ángulo φ con el eje X0, por tanto en el vector  aparece
aparece 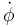 . ¿Pero con qué signo? Cuando el vector
. ¿Pero con qué signo? Cuando el vector  apunta en el sentido positivo del eje Y0 la rotación correspondiente hace aumentar el ángulo, por lo que
apunta en el sentido positivo del eje Y0 la rotación correspondiente hace aumentar el ángulo, por lo que 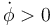 . Para que el sentido del vector y el signo de la derivada sean coherentes tenemos que poner
. Para que el sentido del vector y el signo de la derivada sean coherentes tenemos que poner
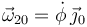
Señalemos que la flecha indicando el sentido del ángulo no influye en el signo que hay que poner. Lo importante es el signo de la derivada del ángulo.
2.1.3 Movimiento {21}
El punto O de la barra se mueve verticalmente. Su velocidad absoluta es
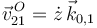
Para el vector rotación aplicamos las leyes de composición
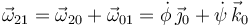
Ya tenemos la reducción cinemática en el punto O. Para obtenerla en el centro de masas de la barra G aplicamos el teorema de Chasles