Barra articulada sobre muelle Enero 2015 (MR G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

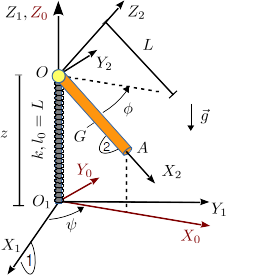
En el sistema de la figura, la barra delgada homogénea $O A$ (sólido "2"), de masa $m$ y longitud $L$ , está articulada en el punto $O$ . El punto $O$ puede moverse sobre el eje fijo $O 1 Z 1$ , y está conectado a un muelle de constante elástica $k$ y longitud natural $L$ . El muelle siempre permanece vertical. La barra "2" está siempre contenida en el plano $O 1 X 0 Z 0$ , como se indica en la figura.

Encuentra la reducción cinemática del movimiento {21} en los puntos $O$ y $G$ .
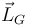Calcula el momento cinético de la barra "2" en $O$ y $G$ ( $\vec{L}_O$ , $\vec{L}_G$ ).
Calcula la energía cinética de la barra "2".
Aplicando el T.C.M. y el T.M.C. escribe las ecuaciones de movimiento del sistema.
Escribe todas las integrales primeras del movimiento que puedas encontrar.

2 Solución

2.1 Reducción cinemática

2.1.1 Movimiento {01}

El punto $O 1$ pertenece al sólido "0" y está siempre en reposo respecto al sólido "1". Por tanto

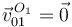
$\vec{v}_{01}^{\,O_1}=\vec{0}$

Para el vector rotación tenemos

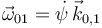
$\vec{\omega}_{01} = \dot{\psi}\,\vec{k}_{0,1}$

2.1.2 Movimiento {20}

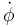De este movimiento realmente sólo nos interesa su vector rotación. El movimiento {20} es un movimiento plano, pues el plano $O X 2 Z 2$ coincide siempre con el plano $O 1 X 0 Z 0$ . El eje de rotación es perpendicular a este plano, es decir, paralelo al eje $Y_2\parallel Y_0$ . El eje $X 2$ forma el ángulo $φ$ con el eje $X 0$ , por tanto en el vector $\vec{\omega}_{20}$ aparece $\dot{\phi}$ . ¿Pero con qué signo? 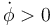Cuando el vector $\vec{\omega}_{20}$ apunta en el sentido positivo del eje $Y 0$ la rotación correspondiente hace aumentar el ángulo, por lo que $\dot{\phi}>0$ . Para que el sentido del vector y el signo de la derivada sean coherentes tenemos que poner

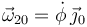
$\vec{\omega}_{20}=\dot{\phi}\,\vec{\jmath}_0$

Señalemos que la flecha indicando el sentido del ángulo no influye en el signo que hay que poner. Lo importante es el signo de la derivada del ángulo.

2.1.3 Movimiento {21}

El punto $O$ de la barra se mueve verticalmente. Su velocidad absoluta es

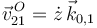
$\vec{v}_{21}^{\,O} = \dot{z}\,\vec{k}_{0,1}$

Para el vector rotación aplicamos las leyes de composición

$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = \dot{\phi}\,\vec{\jmath}_0 + \dot{\psi}\,\vec{k}_0 = [0,\dot{\phi},\dot{\psi}]_0$

Ya tenemos la reducción cinemática en el punto $O$ . Para obtenerla en el centro de masas de la barra $G$ aplicamos el teorema de Chasles

$\vec{v}_{21}^{\,G} = \vec{v}_{21}^{\,O} + \vec{\omega}_{21}\times\overrightarrow{OG} = \left[ -\dfrac{1}{2}L\dot{\phi}\,\mathrm{sen}\,\phi, \dfrac{1}{2}L\dot{\psi}\cos\phi, \dot{z}-\dfrac{1}{2}L\dot{\phi}\cos\phi \right]_0$

2.2 Momento cinético de la barra

Calculamos primero el momento cinético en el centro de masas. El tensor de inercia de la barra en su centro de masas expresado en la base "2" solidaria con la barra es

$\stackrel{\leftrightarrow}{I}_G = I \left[ \begin{array}{ccc} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right]_2$

con $I = m L 2 / 12$ .

El momento cinético respecto al centro de masas es

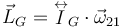
$\vec{L}_G = \stackrel{\leftrightarrow}{I}_G\cdot\vec{\omega}_{21}$

Necesitamos el vector rotación expresado en la base "2". De la figura vemos que

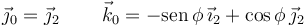
$\vec{\jmath}_0 = \vec{\jmath}_2\, \qquad \vec{k}_0 = -\mathrm{sen}\,\phi\,\vec{\imath}_2 + \cos\phi\,\vec{\jmath}_2$

y entonces el vector rotación es

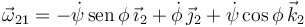
$\vec{\omega}_{21} = -\dot{\psi}\,\mathrm{sen}\,\phi\,\vec{\imath}_2 + \dot{\phi}\,\vec{\jmath}_2 + \dot{\psi}\cos\phi\,\vec{k}_2$

El momento cinético en la base "2" es

$\vec{L}_G = \stackrel{\leftrightarrow}{I}_G\cdot\vec{\omega}_{21} = I \left[ \begin{array}{ccc} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right]_2 \left[ \begin{array}{c} -\dot{\psi}\,\mathrm{sen}\,\phi\\ \dot{\phi}\\ \dot{\psi}\cos\phi\\ \end{array} \right]_2 = [0,I\dot{\phi}, I\dot{\psi}\cos\phi]_2$

En este caso, lo mas fácil para calcular el momento cinético en el punto $O$ es utilizar la expresión del momento cinético en un punto móvil

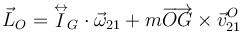
$\vec{L}_O = \stackrel{\leftrightarrow}{I}_G\cdot\vec{\omega}_{21} + m\overrightarrow{OG}\times\vec{v}^O_{21}$

El tensor de inercia en $O$ es

$\stackrel{\leftrightarrow}{I}_O = I_O \left[ \begin{array}{ccc} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right]_2$

con $I O = m L 2 / 3$ . El término asociado al tensor de inercia es

$\stackrel{\leftrightarrow}{I}_O\cdot\vec{\omega}_{21} = I_O \left[ \begin{array}{ccc} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right]_2 \left[ \begin{array}{c} -\dot{\psi}\,\mathrm{sen}\,\phi\\ \dot{\phi}\\ \dot{\psi}\cos\phi\\ \end{array} \right]_2 = [0,I_O\dot{\phi}, I_O\dot{\psi}\cos\phi]_2$

Para el otro término expresamos todos los vectores en la base del sólido "2"

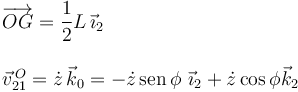
$\begin{array}{l} \overrightarrow{OG} = \dfrac{1}{2}L\,\vec{\imath}_2\\ \\ \vec{v}^{\,O}_{21} = \dot{z}\,\vec{k}_0 = -\dot{z}\,\mathrm{sen}\,\phi\,\,\vec{\imath}_2 + \dot{z}\cos\phi\vec{k}_2 \end{array}$

Entonces

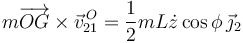
$m\overrightarrow{OG}\times\vec{v}^{\,O}_{21} = \dfrac{1}{2}mL\dot{z}\cos\phi\,\vec{\jmath}_2$

Y el momento cinético en $O$ es

$\vec{L}_O = \left[0, I_O\dot{\phi}+\dfrac{1}{2}mL\dot{z}\cos\phi, I_O\dot{\psi}\cos\phi\right]_2$

Otra posibilidad es calcular el momento cinético en $O$ usando la ecuación del campo de momentos para el momento cinético

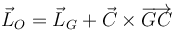
$\vec{L}_O = \vec{L}_G + \vec{C}\times\overrightarrow{GC}$

2.3 Energía cinética de la barra

De nuevo hay varias formas de calcular la energía cinética. Lo mas fácil es pasar por el centro de masas. Así

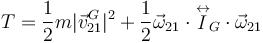
$T = \dfrac{1}{2}m|\vec{v}_{21}^G|^2 + \dfrac{1}{2}\vec{\omega}_{21}\cdot\stackrel{\leftrightarrow}{I}_G\cdot\vec{\omega}_{21}$

El primer término, la energía cinética de traslación, es

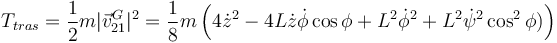
$T_{tras} = \dfrac{1}{2}m|\vec{v}_{21}^G|^2 = \dfrac{1}{8}m \left( 4\dot{z}^2 - 4L\dot{z}\dot{\phi}\cos\phi + L^2\dot{\phi}^2+L^2\dot{\psi}^2\cos^2\phi) \right)$

El término de energía rotación puede calcularse utilizando el momento cinético en $G$ calculado antes

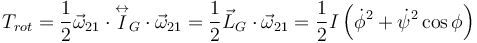
$T_{rot} = \dfrac{1}{2}\vec{\omega}_{21}\cdot\stackrel{\leftrightarrow}{I}_G\cdot\vec{\omega}_{21} = \dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} = \dfrac{1}{2}I\left(\dot{\phi}^2 + \dot{\psi}^2\cos\phi\right)$

La energía cinética total es la suma de los dos términos

$T = T t r a s + T r o t$

2.4 Ecuaciones de movimiento

2.4.1 Fuerzas y pares sobre la barra

Las fuerzas activas que actúan sobre la barra son su peso y la fuerza del muelle. Sus expresiones y el punto en que se aplican son

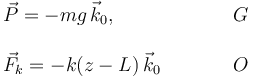
$\begin{array}{lcl} \vec{P} = -mg\,\vec{k}_0, & \qquad & G\\ &&\\ \vec{F}_k = -k(z-L)\,\vec{k}_0 & \qquad & O\\ \end{array}$

Por otro lado, la barra es un sólido vinculado. Recordemos primero que una barra delgada tiene sólo 5 grados de libertad, pues no se consideran rotaciones alrededor de su eje. La reducción cinemática en $O$ tiene como componentes no nulas una de traslación y dos de rotación. Por tanto, en la desvinculación aparecen dos componentes de fuerza para impedir las traslaciones en las direcciones de $X 0$ y $Y 0$ . Así, la barra está sometida a una fuerza de ligadura

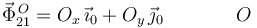
$\begin{array}{lcl} \vec{\Phi}^{\,O}_{21} = O_x\,\vec{\imath}_0 + O_y\,\vec{\jmath}_0&\qquad & O \end{array}$

EL número total de incógnitas es 5

${z (t),φ(t),ψ(t), O x (t), O y (t)}$

Tenemos suficientes ecuaciones para plantear el problema. Recordemos de nuevo que uno de los grados de libertad se pierde.

El T.C.M. queda

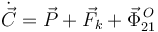
$\dot{\vec{C}} = \vec{P} + \vec{F}_k + \vec{\Phi}^{\,O}_{21}$

De aquí obtenemos tres ecuaciones escalares, una por cada componente.

2.4.2 T.C.M.

La cantidad de movimiento de la barra es

$\vec{C} = m\vec{v}^{\,G}_{21} = \left[ -m\dfrac{1}{2}L\dot{\phi}\,\mathrm{sen}\,\phi, m\dfrac{1}{2}L\dot{\psi}\cos\phi, m(\dot{z}-\dfrac{1}{2}L\dot{\phi}\cos\phi) \right]_0$

La derivada temporal hay que hacerla respecto al sistema absoluto. Como la cantidad de movimiento está expresada en la base "0", hay que aplicar la fórmula de Poisson

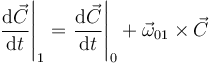
$\left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_1 = \left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_0 + \vec{\omega}_{01}\times\vec{C}$

Tenemos

$\left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_0 = \left[ -\dfrac{1}{2}mL(\ddot{\phi}\,\mathrm{sen}\,\phi + \dot{\phi}^2\cos\phi),\, \dfrac{1}{2}mL(\ddot{\psi}\cos\phi - \dot{\psi}\dot{\phi}\,\mathrm{sen}\,\phi) ,\, m(\ddot{z}-\dfrac{1}{2}L(\ddot{\phi}\cos\phi - \dot{\phi}^2\,\mathrm{sen}\,\phi)) \right]_0$

Por otro lado

$\vec{\omega}_{01}\times\vec{C} = \left[ -\dfrac{1}{2}mL\dot{\psi}^2\cos\phi, \, -\dfrac{1}{2}mL\dot{\psi}\dot{\phi}\,\mathrm{sen}\,\phi, \, 0 \right]_0$

Entonces, las tres ecuaciones escalares que obtenemos del T.C.M son

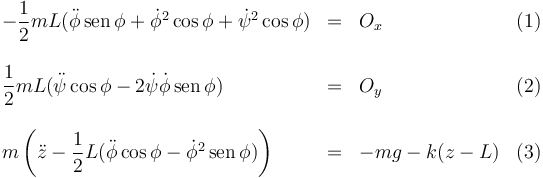
$\begin{array}{lclr} -\dfrac{1}{2}mL(\ddot{\phi}\,\mathrm{sen}\,\phi + \dot{\phi}^2\cos\phi + \dot{\psi}^2\cos\phi) &=& O_x&(1)\\ &&&\\ \dfrac{1}{2}mL(\ddot{\psi}\cos\phi - 2\dot{\psi}\dot{\phi}\,\mathrm{sen}\,\phi) &=& O_y &(2)\\ &&&\\ m\left(\ddot{z}-\dfrac{1}{2}L(\ddot{\phi}\cos\phi - \dot{\phi}^2\,\mathrm{sen}\,\phi)\right) &=& -mg - k(z-L) & (3) \end{array}$

2.4.3 T.M.C.

Aplicamos el T.M.C. en el punto $O$ . Al ser el punto $O$ móvil tenemos

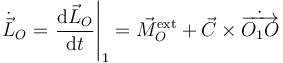
$\dot{\vec{L}}_O = \left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1 = \vec{M}_O^{\mathrm{ext}} + \vec{C}\times\dot{\overrightarrow{O_1O}}$

El momento cinético en $O$ lo hemos calculado en la base "2". Para hacer la derivada temporal respecto de la base "1" tenemos que aplicar una fórmula de Poisson. Pero el cálculo es más sencillo si primero expresamos el momento en la base "0". De la figura vemos que

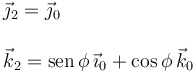
$\begin{array}{l} \vec{\jmath}_2 = \vec{\jmath}_0\\ \\ \vec{k}_2 = \mathrm{sen}\,\phi\,\vec{\imath}_0 + \cos\phi\,\vec{k}_0\\ \end{array}$

por lo que el vector $\vec{L}_O$ expresado en la base "0" es

$\vec{L}_O = \left[ \begin{array}{c} I_O\dot{\psi}\,\mathrm{sen}\,\phi\cos\phi\\ \\ I_O\dot{\phi}+\dfrac{1}{2}mL\dot{z}\cos\phi\\ \\ I_O\dot{\psi}\cos^2\phi \end{array} \right]_0 = \left[ \begin{array}{c} \dfrac{1}{2}I_O\dot{\psi}\,\mathrm{sen}\,(2\phi)\\ \\ I_O\dot{\phi}+\dfrac{1}{2}mL\dot{z}\cos\phi\\ \\ \dfrac{1}{2}I_O\dot{\psi}(1+\cos(2\phi)) \end{array} \right]_0$

La derivada temporal absoluta es

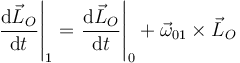
$\left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1 = \left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_0 + \vec{\omega}_{01}\times\vec{L}_O$

Derivamos

$\left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_0 = \left[ \begin{array}{c} \dfrac{1}{2}I_O\,(\ddot{\psi}\,\mathrm{sen}\,(2\phi)+2\dot{\psi}\dot{\phi}\cos(2\phi))\\ \\ I_O\ddot{\phi} + \dfrac{1}{2}mL\,(\ddot{z}\cos\phi-\dot{z}\dot{\phi}\,\mathrm{sen}\,\phi)\\ \\ \dfrac{1}{2}I_O\,(\ddot{\psi}\,(1+\cos(2\phi)) -2\dot{\psi}\dot{\phi}\,\mathrm{sen}\,(2\phi)) \end{array} \right]_0$

El producto vectorial es

$\vec{\omega}_{01}\times\vec{L}_O = \left[ \begin{array}{c} -I_O\dot{\psi}\dot{\phi} -\dfrac{1}{2}mL\dot{z}\dot{\psi}\cos\phi\\ \\ \dfrac{1}{2}I_O\dot{\psi}^2\,\mathrm{sen}\,(2\phi)\\ \\ 0 \end{array} \right]_0$

Es decir, la derivada absoluta del momento cinético en $O$ es

$\left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1 = \left[ \begin{array}{c} \dfrac{1}{2}I_O\,(\ddot{\psi}\,\mathrm{sen}\,(2\phi)+2\dot{\psi}\dot{\phi}(\cos(2\phi) -1)) -\dfrac{1}{2}mL\dot{z}\dot{\psi}\cos\phi\\ \\ \dfrac{1}{2}I_O\,(2\ddot{\phi}+\dot{\psi}^2\,\mathrm{sen}\,(2\phi)) + \dfrac{1}{2}mL\,(\ddot{z}\cos\phi-\dot{z}\dot{\phi}\,\mathrm{sen}\,\phi)\\ \\ \dfrac{1}{2}I_O\,(\ddot{\psi}\,(1+\cos(2\phi)) -2\dot{\psi}\dot{\phi}\,\mathrm{sen}\,(2\phi)) \end{array} \right]_0$

Veamos ahora el lado derecho del T.M.C. Respecto a $O$ , sólo el peso ejerce un momento no nulo. Entonces

$\vec{M}_O^{\mathrm{ext}} = \overrightarrow{OG}\times\vec{P} = \dfrac{1}{2}L\,(\cos\phi\,\vec{\imath}_0 - \mathrm{sen}\,\phi\,\vec{k}_0)\times(-mg\,\vec{k}_0) = \dfrac{1}{2}mgL\cos\phi\,\vec{\jmath}_0 = \left[ \begin{array}{c} 0\\ \\ \dfrac{1}{2}mgL\cos\phi\\ \\ 0 \end{array} \right]_0$

Y para el término extra, presente porque el punto $O$ es móvil, tenemos

$\vec{C}\times\overrightarrow{O_1O} = \vec{C}\times\vec{v}^O_{21} = \left[ \begin{array}{c} \dfrac{1}{2}mL\dot{z}\dot{\psi}\cos\phi\\ \\ \dfrac{1}{2}mL\dot{z}\dot{\psi}\,\mathrm{sen}\,\phi\\ \\ 0 \end{array} \right]_0$

De este modo, el lado derecho del T.C.M. es

$\vec{M}_O^{\mathrm{ext}} + \vec{C}\times\overrightarrow{O_1O} = \left[ \begin{array}{c} \dfrac{1}{2}mL\dot{z}\dot{\psi}\cos\phi\\ \\ \dfrac{1}{2}mgL\cos\phi + \dfrac{1}{2}mL\dot{z}\dot{\psi}\,\mathrm{sen}\,\phi\\ \\ 0 \end{array} \right]_0$

Al igualar la derivada del momento cinético con el lado derecho del T.C.M. obtenemos 3 ecuaciones diferenciales. Las dos primeras, junto con la ecuación (3), son las 3 ecuaciones de movimiento para los grados de libertad ${z,φ,ψ}$

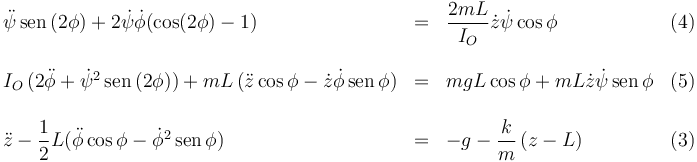
$\begin{array}{lclr} \ddot{\psi}\,\mathrm{sen}\,(2\phi)+2\dot{\psi}\dot{\phi}(\cos(2\phi) -1) &=& \dfrac{2mL}{I_O}\dot{z}\dot{\psi}\cos\phi & (4)\\ &&&\\ I_O\,(2\ddot{\phi}+\dot{\psi}^2\,\mathrm{sen}\,(2\phi)) + mL\,(\ddot{z}\cos\phi-\dot{z}\dot{\phi}\,\mathrm{sen}\,\phi) &=& mgL\cos\phi + mL\dot{z}\dot{\psi}\,\mathrm{sen}\,\phi & (5)\\ &&&\\ \ddot{z}-\dfrac{1}{2}L(\ddot{\phi}\cos\phi - \dot{\phi}^2\,\mathrm{sen}\,\phi) &=& -g - \dfrac{k}{m}\,(z-L) & (3) \end{array}$

Las ecuaciones (1) y (2) dan las componentes de la fuerza de ligadura en el punto $O$

2.5 Integrales primeras de movimiento

La fuerza de ligadura en $O$ es perpendicular a la velocidad del punto $O$ , pues el vínculo es liso. Por tanto, 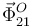$\vec{\Phi}^O_{21}$ no hace trabajo. Las otras dos fuerzas, las de la gravedad y el muelle, son conservativas. Entonces la energía mecánica definida con las energías potenciales asociadas al peso y al muelle se conservan. Estas energías potenciales son

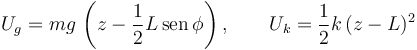
$U_g = mg\,\left(z-\dfrac{1}{2}L\,\mathrm{sen}\,\phi\right), \qquad U_k = \dfrac{1}{2}k\,(z-L)^2$

Hemos escogido como origen de energía potencial gravitatoria la altura correspondiente al plano $O 1 X 1 Y 1$ .

La energía mecánica total, que se conserva, es

$E m = T + U g + U k$

Por otro lado, hay otra magnitud invariante asociada al T.M.C. Como hemos visto, aplicado en $O$ el teorema dice

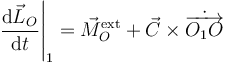
$\left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1 = \vec{M}_O^{\mathrm{ext}} + \vec{C}\times\dot{\overrightarrow{O_1O}}$

En el término del momento sólo interviene el peso, que es paralelo al eje $O 1 Z 0$ . Entonces no tiene componente en ese eje. Además, 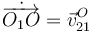$\dot{\overrightarrow{O_1O}}=\vec{v}_{21}^O$ sólo tiene componente en $O 1 Z 0$ , por lo que el producto vectorial 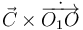$\vec{C}\times\dot{\overrightarrow{O_1O}}$ no tiene componente en $O 1 Z 0$ . Entonces el lado derecho del T.M.C. no tiene componente en $\vec{k}_0$ , por lo que la proyección del momento cinético en $O$ sobre ese eje se conserva. Es decir

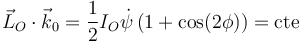
$\vec{L}_O\cdot\vec{k}_0 = \dfrac{1}{2}I_O\dot{\psi}\,(1+\cos(2\phi))=\mathrm{cte}$

Esto ya lo hemos obtenido al aplicar el T.C.M. para obtener las ecuaciones de movimiento (5) y (6). Ahí ya salía que la componente en $O 1 Z 0$ del término derecho del T.M.C. era cero.

Barra articulada sobre muelle Enero 2015 (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática

2.1.1 Movimiento {01}

2.1.2 Movimiento {20}

2.1.3 Movimiento {21}

2.2 Momento cinético de la barra

2.3 Energía cinética de la barra

2.4 Ecuaciones de movimiento

2.4.1 Fuerzas y pares sobre la barra

2.4.2 T.C.M.

2.4.3 T.M.C.

2.5 Integrales primeras de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES