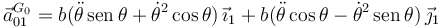Barra empujando placa con vértice fijo (MR G.I.C.)

De Laplace

Revisión a fecha de 23:50 2 nov 2015; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Barra empujando placa con vértice fijo
3 Solución

1 Enunciado

2 Barra empujando placa con vértice fijo

El sistema de sólidos de la figura está formado por una varilla (sólido "2", masa $m$ , longitud 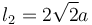$l_2=2\sqrt{2}a$ ) y por una placa cuadrada (sólido "0", masa $m$ , lado $l 0 = 2 a$ ) articulados entre sí en el punto $B$ . Sobre el eje $O X 1$ se apoyan el extremo $A$ de la barra y el lado $B D$ del cuadrado. Todos los contactos son lisos, salvo el apoyo del cuadrado, donde el coeficiente de rozamiento $μ$ es tal que el deslizamiento es imposible. Sobre el extremo $A$ se aplica una fuerza horizontal creciente 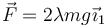$\vec{F}=2\lambda mg\vec{\imath}_1$ donde $λ$ es un parámetro del problema. Inicialmente $A$ coincide con $O$ .

Obtén el sistema de ecuaciones que permite determinar la ecuación diferencial del movimiento y las fuerzas vinculares del problema.
Suponiendo $λ = λ 0 (c t e .)$ , demuestra que el trabajo de $\vec{F}$ es conservativo, con una energía potencial $V F (x) = - F 0 x$ , donde $F 0 = 2λ 0 m g$ . Obtén el movimiento del sistema en forma de integral primera, suponiendo reposo inicial.

3 Solución

3.1 Geometría del problema

En la figura de la izquierda se muestra la relación entre los parámetros geométricos $x$ , $θ$ y $ψ$ . Llamamos 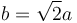$b=\sqrt{2}a$ . La barra y la diagonal $B' D$ de la placa forman siempre un triángulo isósceles. Vemos entonces que la relación entre los ángulos es

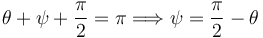
$\theta + \psi + \dfrac{\pi}{2}=\pi \Longrightarrow \psi = \dfrac{\pi}{2} - \theta$

Por otro lado, en $t = 0$ el punto $A$ estaba sobre $O$ , y la placa estaba completamente apoyada sobre el eje $O X 1$ . Por tanto $θ(0) = π / 4$ y 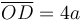$\overline{OD} = 4a$ . Entonces

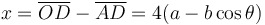
$x = \overline{OD} - \overline{AD} = 4(a-b\cos\theta)$

Vemos que el movimiento está descrito por un sólo grado de libertad. Escogeremos el ángulo $θ$ para describirlo

3.2 Cinemática del problema

Tanto el sólido "2" como el "0" describen una rotación plana. Vamos a encontrar las reducciones cinemáticas de estos movimientos.

Movimiento {21}

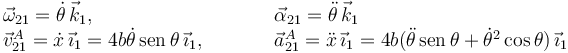
$\begin{array}{lcl} \vec{\omega}_{21} = \dot{\theta}\,\vec{k}_1, & \qquad & \vec{\alpha}_{21} = \ddot{\theta}\,\vec{k}_1\\ \vec{v}^A_{21} = \dot{x}\,\vec{\imath}_1 = 4b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1, &\qquad & \vec{a}^A_{21} = \ddot{x}\,\vec{\imath}_1 = 4b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 \end{array}$

Necesitaremos la aceleración en el centro de masas de la barra:

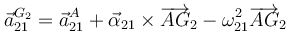
$\vec{a}^{G_2}_{21} = \vec{a}^A_{21} + \vec{\alpha}_{21}\times\overrightarrow{AG}_2 - \omega_{21}^2\overrightarrow{AG}_2$

Hemos utilizado la versión simplificada de la ecuación del campo de aceleraciones, pues el movimiento es plano. El vector geométrico es

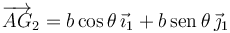
$\overrightarrow{AG}_2 = b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Operando llegamos a

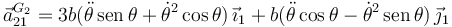
$\vec{a}^{G_2}_{21} = 3b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 + b(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1$

Movimiento {01}

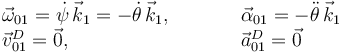
$\begin{array}{lcl} \vec{\omega}_{01} = \dot{\psi}\,\vec{k}_1 = -\dot{\theta}\,\vec{k}_1, & \qquad & \vec{\alpha}_{01} = -\ddot{\theta}\,\vec{k}_1\\ \vec{v}^D_{01} = \vec{0}, &\qquad & \vec{a}^D_{01} = \vec{0} \end{array}$

Necesitaremos la aceleración en el centro de masas de la placa:

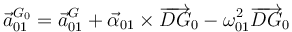
$\vec{a}^{G_0}_{01} = \vec{a}^G_{01} + \vec{\alpha}_{01}\times\overrightarrow{DG}_0 - \omega_{01}^2\overrightarrow{DG}_0$

De nuevo el movimiento es plano. El vector geométrico es

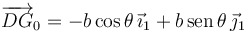
$\overrightarrow{DG}_0 = -b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Operando llegamos a

$\vec{a}^{G_0}_{01} = b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 + b(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1$

Barra empujando placa con vértice fijo (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Barra empujando placa con vértice fijo

3 Solución

3.1 Geometría del problema

3.2 Cinemática del problema

3.3 Fuerzas sobre las placas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES