Barra empujando placa con vértice fijo (MR G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Barra empujando placa con vértice fijo
3 Solución

1 Enunciado

2 Barra empujando placa con vértice fijo

El sistema de sólidos de la figura está formado por una varilla (sólido "2", masa $m$ , longitud 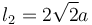$l_2=2\sqrt{2}a$ ) y por una placa cuadrada (sólido "0", masa $m$ , lado $l 0 = 2 a$ ) articulados entre sí en el punto $B$ . Sobre el eje $O X 1$ se apoyan el extremo $A$ de la barra y el lado $B D$ del cuadrado. Todos los contactos son lisos, salvo el apoyo del cuadrado, donde el coeficiente de rozamiento $μ$ es tal que el deslizamiento es imposible. Sobre el extremo $A$ se aplica una fuerza horizontal 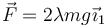$\vec{F}=2\lambda mg\vec{\imath}_1$ donde $λ$ es un parámetro del problema. Inicialmente $A$ coincide con $O$ .

Obtén el sistema de ecuaciones que permite determinar la ecuación diferencial del movimiento y las fuerzas vinculares del problema.
Suponiendo $λ = λ 0 (c t e .)$ , demuestra que el trabajo de $\vec{F}$ es conservativo, con una energía potencial $V F (x) = - F 0 x$ , donde $F 0 = 2λ 0 m g$ . Obtén el movimiento del sistema en forma de integral primera, suponiendo reposo inicial.

3 Solución

3.1 Geometría del problema

En la figura de la izquierda se muestra la relación entre los parámetros geométricos $x$ , $θ$ y $ψ$ . Llamamos 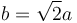$b=\sqrt{2}a$ . La barra y la diagonal $B' D$ de la placa forman siempre un triángulo isósceles. Vemos entonces que la relación entre los ángulos es

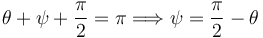
$\theta + \psi + \dfrac{\pi}{2}=\pi \Longrightarrow \psi = \dfrac{\pi}{2} - \theta$

Por otro lado, en $t = 0$ el punto $A$ estaba sobre $O$ , y la placa estaba completamente apoyada sobre el eje $O X 1$ . Por tanto $θ(0) = π / 4$ y 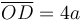$\overline{OD} = 4a$ . Entonces

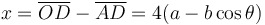
$x = \overline{OD} - \overline{AD} = 4(a-b\cos\theta)$

Vemos que el movimiento está descrito por un sólo grado de libertad. Escogeremos el ángulo $θ$ para describirlo

3.2 Cinemática del problema

Tanto el sólido "2" como el "0" describen una rotación plana. Vamos a encontrar las reducciones cinemáticas de estos movimientos.

Movimiento {21}

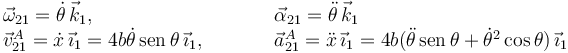
$\begin{array}{lcl} \vec{\omega}_{21} = \dot{\theta}\,\vec{k}_1, & \qquad & \vec{\alpha}_{21} = \ddot{\theta}\,\vec{k}_1\\ \vec{v}^A_{21} = \dot{x}\,\vec{\imath}_1 = 4b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1, &\qquad & \vec{a}^A_{21} = \ddot{x}\,\vec{\imath}_1 = 4b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 \end{array}$

Necesitaremos la velocidad y la aceleración en el centro de masas de la barra:

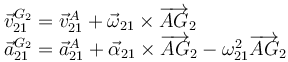
$\begin{array}{l} \vec{v}^{G_2}_{21} = \vec{v}^A_{21} + \vec{\omega}_{21}\times\overrightarrow{AG}_2\\ \vec{a}^{G_2}_{21} = \vec{a}^A_{21} + \vec{\alpha}_{21}\times\overrightarrow{AG}_2 - \omega_{21}^2\overrightarrow{AG}_2 \end{array}$

Hemos utilizado la versión simplificada de la ecuación del campo de aceleraciones, pues el movimiento es plano. El vector geométrico es

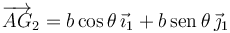
$\overrightarrow{AG}_2 = b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Operando llegamos a

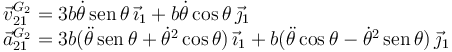
$\begin{array}{l} \vec{v}^{G_2}_{21} = 3b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + b\dot{\theta}\cos\theta\,\vec{\jmath}_1\\ \vec{a}^{G_2}_{21} = 3b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 + b(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1 \end{array}$

Movimiento {01}

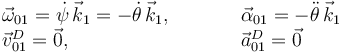
$\begin{array}{lcl} \vec{\omega}_{01} = \dot{\psi}\,\vec{k}_1 = -\dot{\theta}\,\vec{k}_1, & \qquad & \vec{\alpha}_{01} = -\ddot{\theta}\,\vec{k}_1\\ \vec{v}^D_{01} = \vec{0}, &\qquad & \vec{a}^D_{01} = \vec{0} \end{array}$

Necesitaremos la aceleración en el centro de masas de la placa:

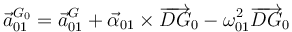
$\vec{a}^{G_0}_{01} = \vec{a}^G_{01} + \vec{\alpha}_{01}\times\overrightarrow{DG}_0 - \omega_{01}^2\overrightarrow{DG}_0$

De nuevo el movimiento es plano. El vector geométrico es

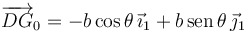
$\overrightarrow{DG}_0 = -b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Operando llegamos a

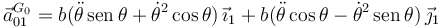
$\vec{a}^{G_0}_{01} = b(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 + b(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1$

3.3 Fuerzas sobre las placas

La figura de la derecha muestra las fuerzas que actúan sobre cada sólido. Vamos a expresarlas en el sistema $O X 1 Y 1$ .

Para el sólido "0"

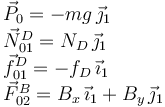
$\begin{array}{l} \vec{P}_0 = -mg\,\vec{\jmath}_1\\ \vec{N}^D_{01} = N_D\,\vec{\jmath}_1\\ \vec{f}^D_{01} = -f_D\,\vec{\imath}_1\\ \vec{F}^B_{02} = B_x\,\vec{\imath}_1 + B_y\,\vec{\jmath}_1 \end{array}$

Para el sólido "2" tenemos

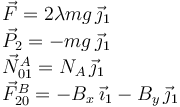
$\begin{array}{l} \vec{F} = 2\lambda mg\,\vec{\jmath}_1\\ \vec{P}_2 = -mg\,\vec{\jmath}_1\\ \vec{N}^A_{01} = N_A\,\vec{\jmath}_1\\ \vec{F}^B_{20} = -B_x\,\vec{\imath}_1 - B_y\,\vec{\jmath}_1 \end{array}$

3.4 Ecuaciones de movimiento

Tenemos 6 incógnitas en el problema, a saber

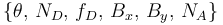
$\{\theta,\, N_D,\, f_D,\, B_x,\, B_y,\, N_A\}$

Aplicando el T.C.M. y el T.M.C. en cada sólido obtenemos 6 ecuaciones, por lo que podemos resolver el problema.

3.4.1 Sólido "2"

T.C.M. en el sólido "2"

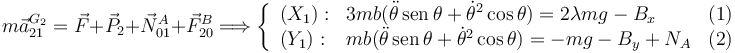
$m\vec{a}^{G_2}_{21} = \vec{F} + \vec{P}_2 + \vec{N}^A_{01} + \vec{F}^B_{20} \Longrightarrow \left\{ \begin{array}{llr} (X_1): & 3mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = 2\lambda mg - B_x & (1)\\ (Y_1): & mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = -mg - B_y + N_A & (2) \end{array} \right.$

Aplicamos el T.M.C. en el centro de masas

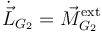
$\dot{\vec{L}}_{G_2} = \vec{M}^{\mathrm{ext}}_{G_2}$

La derivada del momento cinético es

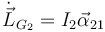
$\dot{\vec{L}}_{G_2} = I_2 \vec{\alpha}_{21}$

El momento de inercia es el de una barra respecto a un eje perpendicular a ella que pasa por su centro de masas

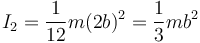
$I_2 = \dfrac{1}{12}m(2b)^2 = \dfrac{1}{3}mb^2$

Para los momentos tenemos

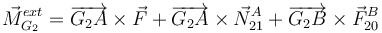
$\vec{M}^{ext}_{G_2} = \overrightarrow{G_2A}\times\vec{F} + \overrightarrow{G_2A}\times\vec{N}_{21}^A + \overrightarrow{G_2B}\times\vec{F}_{20}^B$

Los vectores geométricos son

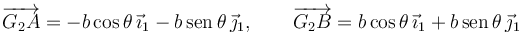
$\overrightarrow{G_2A} = -b\cos\theta\,\vec{\imath}_1 - b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1, \qquad \overrightarrow{G_2B} = b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Operando tenemos

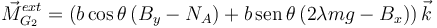
$\vec{M}^{ext}_{G_2} = (b\cos\theta\,(B_y-N_A) + b\,\mathrm{sen}\,\theta\,(2\lambda mg - B_x))\,\vec{k}$

Aplicando el T.M.C. tenemos

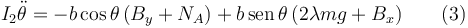
$I_2\ddot{\theta} = -b\cos\theta\,(B_y+N_A) + b\,\mathrm{sen}\,\theta\,(2\lambda mg + B_x) \qquad (3)$

3.4.2 Sólido "0"

T.C.M. en el sólido "0"

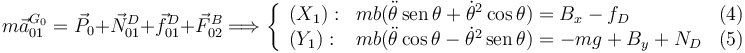
$m\vec{a}^{G_0}_{01} = \vec{P}_0 + \vec{N}^D_{01} + \vec{f}_{01}^D + \vec{F}^B_{02} \Longrightarrow \left\{ \begin{array}{llr} (X_1): & mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = B_x - f_D & (4)\\ (Y_1): & mb(\ddot{\theta}\cos\theta- \dot{\theta}^2\,\mathrm{sen}\,\theta ) = -mg + B_y + N_D & (5) \end{array} \right.$

Aplicamos el T.M.C. en el punto $D$ , que es un punto fijo

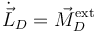
$\dot{\vec{L}}_{D} = \vec{M}^{\mathrm{ext}}_{D}$

La derivada del momento cinético es

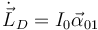
$\dot{\vec{L}}_{D} = I_0 \vec{\alpha}_{01}$

El momento de inercia es el de una placa cuadrada respecto a un eje perpendicular a ella que pasa por el vértice $D$ . El momento de inercia respecto a un eje perpendicular a la placa cuadrada que pasa por se su centro de masas es

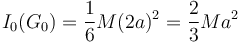
$I_0(G_0) = \dfrac{1}{6}M(2a)^2 = \dfrac{2}{3}Ma^2$

Usando el teorema de Steiner el momento de inercia respecto a un eje que pasa por $D$ es

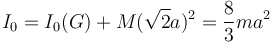
$I_0 = I_0(G) + M(\sqrt{2}a)^2 = \dfrac{8}{3}ma^2$

Entonces

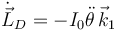
$\dot{\vec{L}}_{D} = -I_0\ddot{\theta}\,\vec{k}_1$

Para los momentos tenemos

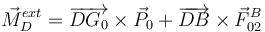
$\vec{M}^{ext}_{D} = \overrightarrow{DG_0}\times\vec{P}_{0} + \overrightarrow{DB}\times\vec{F}_{02}^B$

Los vectores geométricos son

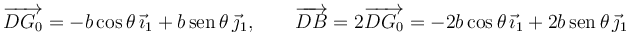
$\overrightarrow{DG_0} = -b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1, \qquad \overrightarrow{DB} = 2\overrightarrow{DG_0} = -2b\cos\theta\,\vec{\imath}_1 + 2b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Recordemos que la diagonal de la placa es 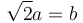$\sqrt{2}a=b$ . Operando tenemos

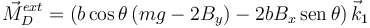
$\vec{M}^{ext}_{D} = (b\cos\theta\,(mg-2B_y) - 2bB_x\,\mathrm{sen}\,\theta)\,\vec{k}_1$

Aplicando el T.M.C. tenemos

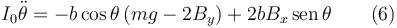
$I_0\ddot{\theta} = -b\cos\theta\,(mg-2B_y) + 2bB_x\,\mathrm{sen}\,\theta \qquad (6)$

3.4.3 Ecuaciones

Reunimos aquí las seis ecuaciones que hemos encontrado

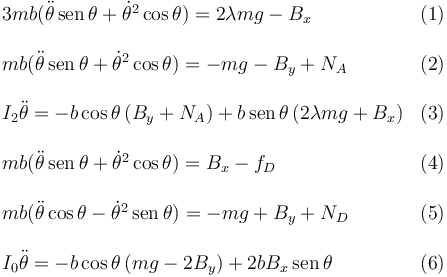
$\begin{array}{lr} 3mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = 2\lambda mg - B_x & (1)\\ & \\ mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = -mg - B_y + N_A & (2)\\ & \\ I_2\ddot{\theta} = -b\cos\theta\,(B_y+N_A) + b\,\mathrm{sen}\,\theta\,(2\lambda mg + B_x) & (3)\\ & \\ mb(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = B_x - f_D & (4)\\ & \\ mb(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta) = -mg + B_y + N_D & (5)\\ & \\ I_0\ddot{\theta} = -b\cos\theta\,(mg-2B_y) + 2bB_x\,\mathrm{sen}\,\theta & (6) \end{array}$

3.5 Caso con $λ$ constante

Si $λ = λ 0$ , constante, la fuerza es

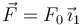
$\vec{F} = F_0\,\vec{\imath}_1$

con $F 0 = 2λ 0 m g$ . El trabajo realizado por la fuerza en un desplazamiento infinitesimal del punto $A$ es

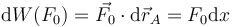
$\mathrm{d}W(F_0) = \vec{F_0}\cdot\mathrm{d}\vec{r}_A = F_0\mathrm{d}x$

Para que sea potencial debe ocurrir que

$d V F = - d W (F 0) = - F 0 d x$

sea integrable. Como $F 0$ es constante tenemos

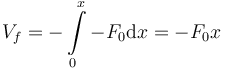
$V_f = -\int\limits_0^x -F_0\mathrm{d}x = -F_0x$

Hemos tomado como referencia de energía potencial $V F (x = 0) = 0$ . Las fuerzas sobre la placa en $D$ no realizan trabajo, pues el punto $D$ es fijo. Entonces sólo $\vec{F}_0$ y el peso de los dos sólidos realizan trabajo. Como son todas fuerzas conservativas, la energía mecánica total se conserva

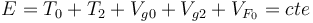
$E = T_0 + T_2 + V_{g0} + V_{g2} + V_{F_0} = cte$

Calculamos los términos de la energía mecánica. Para la barra tenemos

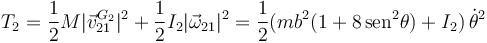
$T_2 = \dfrac{1}{2}M|\vec{v}^{G_2}_{21}|^2 + \dfrac{1}{2}I_2|\vec{\omega}_{21}|^2 = \dfrac{1}{2}(mb^2(1+8\,\mathrm{sen}^2\theta)+I_2)\,\dot{\theta}^2$

Para la placa, al ser $D$ un punto fijo,

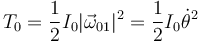
$T_0 = \dfrac{1}{2}I_0|\vec{\omega}_{01}|^2 = \dfrac{1}{2}I_0\dot{\theta}^2$

Las energías potenciales gravitatorias son, tomando como referencia $y = 0$ ,

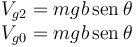
$\begin{array}{l} V_{g2} = mgb\,\mathrm{sen}\,\theta\\ V_{g0} = mgb\,\mathrm{sen}\,\theta \end{array}$

Y la energía potencial asociada a $\vec{F}_0$ es

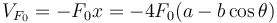
$V_{F_0} = -F_0x = -4F_0(a-b\cos\theta)$

Por tanto la integral primera es

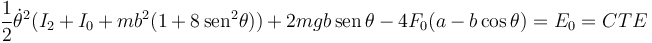
$\dfrac{1}{2}\dot{\theta}^2(I_2+I_0+mb^2(1+8\,\mathrm{sen}^2\theta)) + 2mgb\,\mathrm{sen}\,\theta - 4F_0(a-b\cos\theta) = E_0 = CTE$

La constante se determina evaluando la energía mecánica con las condiciones iniciales. Si parte del reposo y $A$ coincidía con $O$ tendríamos

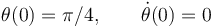
$\theta(0) = \pi/4, \qquad \dot{\theta}(0) = 0$

y

$E_0 = \sqrt{2}mgb - 4F_0(a-b/\sqrt{2}) = 2mga$

Barra empujando placa con vértice fijo (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Barra empujando placa con vértice fijo

3 Solución

3.1 Geometría del problema

3.2 Cinemática del problema

3.3 Fuerzas sobre las placas

3.4 Ecuaciones de movimiento

3.4.1 Sólido "2"

3.4.2 Sólido "0"

3.4.3 Ecuaciones

3.5 Caso con $λ$ constante

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra empujando placa con vértice fijo (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Barra empujando placa con vértice fijo

3 Solución

3.1 Geometría del problema

3.2 Cinemática del problema

3.3 Fuerzas sobre las placas

3.4 Ecuaciones de movimiento

3.4.1 Sólido "2"

3.4.2 Sólido "0"

3.4.3 Ecuaciones

3.5 Caso con λ constante

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

3.5 Caso con $λ$ constante