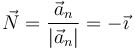Entrar Página Discusión Historial Go to the site toolbox

Partícula unida a un sistema articulado

De Laplace

Contenido

1 Enunciado

Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud h situadas sobre una superficie horizontal. La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular − 2Ω. En el instante t = 0 el sistema está completamente extendido a lo largo del eje OX.

  1. Escriba las ecuaciones horarias de la posición del punto B para todo instante.
  2. Para el instante t = 0 halle
    1. La velocidad y la rapidez.
    2. La aceleración como vector y sus componentes intrínsecas (escalares).
    3. El radio y el centro de curvatura.
  3. Para el instante t = π / (2Ω) calcule
    1. La velocidad y la rapidez.
    2. La aceleración como vector y sus componentes intrínsecas (escalares).
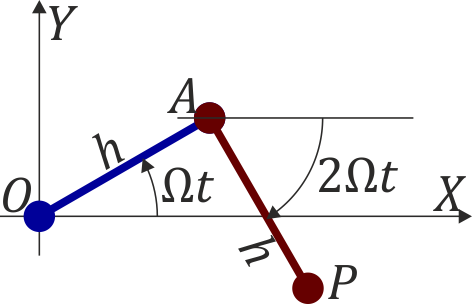
Archivo:barras-articuladas-rotatorias-2.png

2 Ecuaciones horarias

Podemos halalr la posición instantánea mediante una suma vectorial

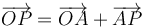
\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}

siendo

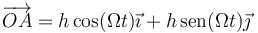
\overrightarrow{OA}=h\cos(\Omega t)\vec{\imath}+h\,\mathrm{sen}(\Omega t)\vec{\jmath}

y

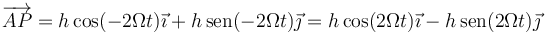
\overrightarrow{AP}=h\cos(-2\Omega t)\vec{\imath}+h\,\mathrm{sen}(-2\Omega t)\vec{\jmath}=h\cos(2\Omega t)\vec{\imath}-h\,\mathrm{sen}(2\Omega t)\vec{\jmath}

lo que da

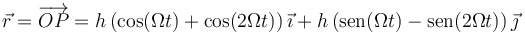
\vec{r}=\overrightarrow{OP}=h\left(\cos(\Omega t)+\cos(2\Omega t)\right)\vec{\imath}+h\left(\mathrm{sen}(\Omega t)-\mathrm{sen}(2\Omega t)\right)\vec{\jmath}

Una vez que tenemos el vector de posición, calculamos la velocidad instantánea derivando una vez respecto al tiempo

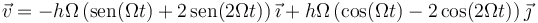
\vec{v}=-h\Omega\left(\mathrm{sen}(\Omega t)+2\,\mathrm{sen}(2\Omega t)\right)\vec{\imath}+h\Omega\left(\cos(\Omega t)-2\cos(2\Omega t)\right)\vec{\jmath}

y la aceleración derivando una seguna vez

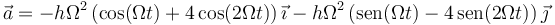
\vec{a}=-h\Omega^2\left(\mathrm{cos}(\Omega t)+4\,\mathrm{cos}(2\Omega t)\right)\vec{\imath}-h\Omega^2\left(\mathrm{sen}(\Omega t)-4\,\mathrm{sen}(2\Omega t)\right)\vec{\jmath}

3 Magnitudes en t=0

Si particularizamos los resultados generales para el instante t = 0 nos queda

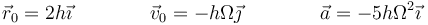
\vec{r}_0=2h\vec{\imath}\qquad\qquad \vec{v}_0=-h\Omega\vec{\jmath}\qquad\qquad \vec{a}=-5h\Omega^2\vec{\imath}

sin más que aplicar que sen(0) = 0 y cos(0) = 1.

3.1 Velocidad y rapidez

La velocidad ya la tenemos

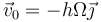
\vec{v}_0=-h\Omega\vec{\jmath}

y la rapidez o celeridad es el módulo de esta

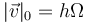
|\vec{v}|_0=h\Omega

De camino, obtenemos el vector tangente en este instante

\vec{T}_0=\frac{\vec{v}_0}{|\vec{v}|_0}=-\vec{\jmath}

3.2 Aceleración

El vector aceleración ya lo tenemos

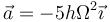
\vec{a}=-5h\Omega^2\vec{\imath}

Esta aceleración es ortogonal a la velocidad instantánea, por tanto se anula la aceleración tangencial en este instante.

\vec{a}_t=\vec{0}\qquad\qquad a_t=0

y la aceleración normal coincide con la aceleración al completo

\vec{a}_n=\vec{a}=-5h\Omega^2\vec{\imath}\qquad\qquad a_n = |\vec{a}_n|=5h\Omega^2

El vector normal en este instante es el unitario en la dirección y sentido de la aceleración normal

\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\vec{\imath}

4 Magnitudes en t = π/(2Ω)

Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_unida_a_un_sistema_articulado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace