Sistema de 5 resistencias

De Laplace

1 Enunciado

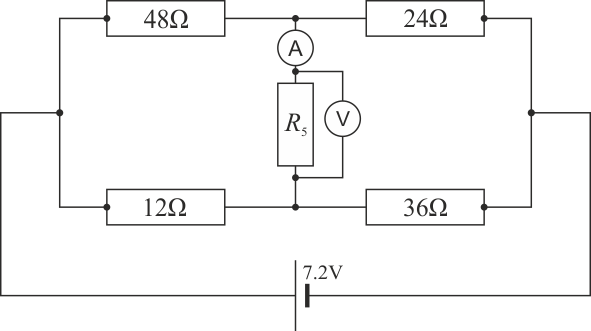
Se tiene el sistema de 5 resistencias de la figura. Entre los extremos de la asociación se aplica una diferencia de potencial de 7.2 V.

Determine las lecturas del amperímetro y voltímetro de la rama central en los casos:

1. 
2. 
3. 
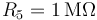
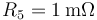
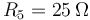
4. El valor de R₅ que haga máxima la potencia disipada en ella por efecto Joule.

2 Introducción

Este problema guarda una notable similitud con el de las 4 bombillas, con el añadido de la resistencia central.

En el primer supuesto de este problema, la resistencia central es gigantesca comparada con el resto, por lo que se puede suponer que esa rama se encuentra en circuito abierto, es decir, que no circula corriente por ella. Este caso se reduce al primero del sistema de cuatro bombillas.

En el segundo caso, la resistencia central es minúscula comparada con las otras dos, por lo que se puede tratar como un cortocircuito, es decir, la diferencia de potencial en esa rama es nula. Este caso se reduce al segundo del sistema de cuatro bombillas.

En el tercer caso, la resistencia central es comparable a las otras cuatro, por lo que el sistema no se reduce a los casos anteriores y hay que resolverlo en su integridad.

Para el cuarto caso, no conocemos la resistencia intermedia, por lo que también es precisa la solución completa.

Los dos primeros casos pueden resolverse reduciendo el sistema a asociaciones en serie o en paralelo de cuatro resistencias, como en el mencionado problema de las 4 bombillas. Para no repetir soluciones, aquí plantearemos una solución general, que luego resolveremos para los casos concretos.

2.1 Planteamiento general

En primer lugar, etiquetamos los nodos. Sean A y B los nodos a los que está conectada la fuente y D y E los nodos a los que está unida la resistencia central (siendo D el superior).

Sean R₁ y R₂ las resistencias de la rama superior y R₃ y R₄ las de la rama inferior, es decir

En lo que sigue, mediremos todas las resistencias en ohmios, todas las intensidades de corriente en amperios y todas las diferencias de potencial en voltios.

Teniendo esto en cuenta, nos queda, por aplicación de la ley de Ohm a cada resistencia

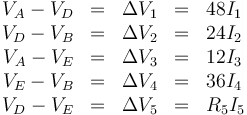
A estas ecuaciones hay que añadir que conocemos la diferencia de potencial entre los extremos

y, que de acuerdo con la ley de Kirchhoff para los nodos

A partir de estas ecuaciones podemos determinar completamente topdas las intensidades de corriente y diferencias de potencial. Sin embargo, es más sencillo comenzar por los dos casos particulares de cirucito abierto y cortocircuito.

3 Circuito abierto

4 Cortocircuito

5 Caso intermedio

6 Máxima potencia