Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Cuestión sobre EIRMD II (Ex.Sep/14)

De Laplace

1 Enunciado

2 No Boletín - Cuestión sobre EIRMD II (Ex.Sep/14)

El campo de velocidades de un sólido rígido en movimiento helicoidal instantáneo (respecto a un triedro OXYZ de referencia) está definido mediante la siguiente reducción cinemática:

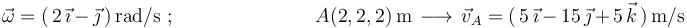
\vec{\omega}=(\,2\,\vec{\imath}\,-\,\vec{\jmath}\,)\,\mathrm{rad}/\mathrm{s}\,\,;\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, A(2,2,2)\,\mathrm{m} \,\longrightarrow\, \vec{v}_A=(\,5\,\vec{\imath}\,-\,15\,\vec{\jmath}\,+\,5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s}

¿Por cuál de los siguientes puntos pasa el eje instantáneo de rotación y mínimo deslizamiento?

\mathrm{(a)}\,\,\,\,\mathrm{I(1,0,-3)}\,\mathrm{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(b)}\,\,\,\,\mathrm{I(2,-1,-3)}\,\mbox{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(c)}\,\,\,\,\mathrm{I(-1,-2,-5)}\,\mbox{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(d)}\,\,\,\,\mathrm{I(2,2,2)}\,\mbox{m}

3 Solución

Mediante la ecuación del campo de velocidades del sólido rígido, podemos calcular la velocidad del punto 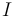I\, en cada una de las opciones:

\begin{array}{lll} \mathrm{(a)}\,\,\,\,\,\overrightarrow{AI}=(-\vec{\imath}-2\,\vec{\jmath}-5\,\vec{k}\,)\,\mathrm{m} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ -1 & -2 & -5 \end{array}\right|=(\,10\,\vec{\imath}-5\,\vec{\jmath}\,\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(b)}\,\,\,\,\,\overrightarrow{AI}=(-3\,\vec{\jmath}-5\,\vec{k}\,)\,\mathrm{m}& \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ 0 & -3 & -5 \end{array}\right|=(\,10\,\vec{\imath}-5\,\vec{\jmath}-\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(c)}\,\,\,\,\,\overrightarrow{AI}=(-3\,\vec{\imath}-4\,\vec{\jmath}-7\,\vec{k}\,)\,\mathrm{m}& \,\,\longrightarrow\,\,\,\,\, &\vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ -3 & -4 & -7 \end{array}\right|=(\,12\,\vec{\imath}-\vec{\jmath}-6\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(d)}\,\,\,\,\,\overrightarrow{AI}=\vec{0}\,\mathrm{m} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ 0 & 0 & 0 \end{array}\right|=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \end{array}

Si el punto 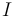I\, pertenece al eje instantáneo de rotación y mínimo deslizamiento (EIRMD), la velocidad 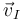\vec{v}_I\, de dicho punto ha de ser necesariamente paralela al vector velocidad angular 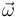\vec{\omega}\, (producto vectorial nulo). Comprobamos a continuación que tal cosa sólo ocurre en la opción (a), y por tanto esa es la respuesta correcta:

\begin{array}{lll} \mathrm{(a)}\,\,\,\,\,\vec{v}_I=(\,10\,\vec{\imath}-5\,\vec{\jmath}\,\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 10 & -5 & 0 \\ 2 & -1 & 0 \end{array}\right|=\vec{0}\,\,\,\longrightarrow\,\,\,\,\,\vec{v}_I\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\in \mathrm{EIRMD} \\ \\ \mathrm{(b)}\,\,\,\,\,\vec{v}_I=(\,10\,\vec{\imath}-5\,\vec{\jmath}-\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 10 & -5 & -1 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0} \,\,\,\longrightarrow\,\,\,\,\,\vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \\ \\ \mathrm{(c)}\,\,\,\,\,\vec{v}_I=(\,12\,\vec{\imath}-\vec{\jmath}-6\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 12 & -1 & -6 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0} \,\,\,\longrightarrow\,\,\,\,\,\vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \\ \\ \mathrm{(d)}\,\,\,\,\,\vec{v}_I=(\,5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 5 & -15 & 5 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0}\,\,\,\longrightarrow\,\,\,\,\,\vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \end{array}
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Cuesti%C3%B3n_sobre_EIRMD_II_(Ex.Sep/14)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace