No Boletín - Cuestión sobre EIRMD II (Ex.Sep/14)

De Laplace

1 Enunciado

El campo de velocidades de un sólido rígido en movimiento helicoidal instantáneo (respecto a un triedro OXYZ de referencia) está definido mediante la siguiente reducción cinemática:

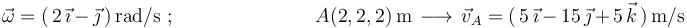
$\vec{\omega}=(\,2\,\vec{\imath}\,-\,\vec{\jmath}\,)\,\mathrm{rad}/\mathrm{s}\,\,;\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, A(2,2,2)\,\mathrm{m} \,\longrightarrow\, \vec{v}_A=(\,5\,\vec{\imath}\,-\,15\,\vec{\jmath}\,+\,5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s}$

¿Por cuál de los siguientes puntos pasa el eje instantáneo de rotación y mínimo deslizamiento?

$\mathrm{(a)}\,\,\,\,I\mathrm{(1,0,-3)}\,\mathrm{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(b)}\,\,\,\,I\mathrm{(2,-1,-3)}\,\mbox{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(c)}\,\,\,\,I\mathrm{(-1,-2,-5)}\,\mbox{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(d)}\,\,\,\,I\mathrm{(2,2,2)}\,\mbox{m}$

2 Primer método: cálculo de la velocidad del punto 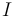$I\,$

Utilizando la ecuación del campo de velocidades del sólido rígido, calculamos la velocidad 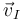$\vec{v}_I\,$ del punto 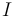$I\,$ en cada una de las opciones:

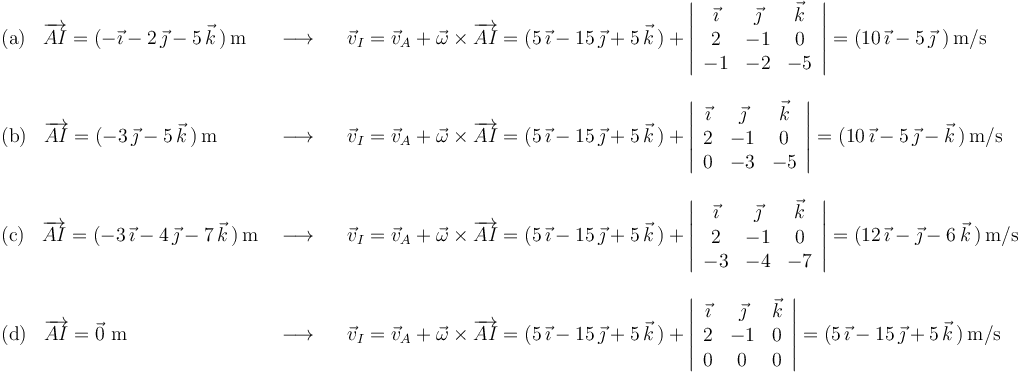
$\begin{array}{lll} \mathrm{(a)}\,\,\,\,\,\overrightarrow{AI}=(-\vec{\imath}-2\,\vec{\jmath}-5\,\vec{k}\,)\,\mathrm{m} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ -1 & -2 & -5 \end{array}\right|=(10\,\vec{\imath}-5\,\vec{\jmath}\,\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(b)}\,\,\,\,\,\overrightarrow{AI}=(-3\,\vec{\jmath}-5\,\vec{k}\,)\,\mathrm{m}& \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ 0 & -3 & -5 \end{array}\right|=(10\,\vec{\imath}-5\,\vec{\jmath}-\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(c)}\,\,\,\,\,\overrightarrow{AI}=(-3\,\vec{\imath}-4\,\vec{\jmath}-7\,\vec{k}\,)\,\mathrm{m}& \,\,\longrightarrow\,\,\,\,\, &\vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ -3 & -4 & -7 \end{array}\right|=(12\,\vec{\imath}-\vec{\jmath}-6\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \\ \mathrm{(d)}\,\,\,\,\,\overrightarrow{AI}=\vec{0}\,\,\mathrm{m} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I=\vec{v}_A+\vec{\omega}\times\overrightarrow{AI}=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ 0 & 0 & 0 \end{array}\right|=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} \\ \end{array}$

Si el punto 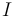$I\,$ pertenece al eje instantáneo de rotación y mínimo deslizamiento (EIRMD), la velocidad 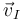$\vec{v}_I\,$ de dicho punto es necesariamente paralela al vector velocidad angular 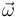$\vec{\omega}\,$ . Comprobamos que tal cosa sólo ocurre en la opción (a), la cual es por tanto la respuesta correcta:

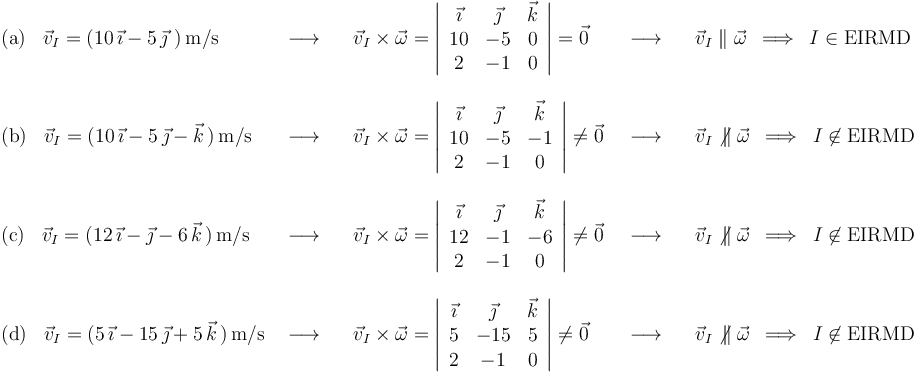
$\begin{array}{lllll} \mathrm{(a)}\,\,\,\,\,\vec{v}_I=(10\,\vec{\imath}-5\,\vec{\jmath}\,\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 10 & -5 & 0 \\ 2 & -1 & 0 \end{array}\right|=\vec{0} & \,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\in \mathrm{EIRMD} \\ \\ \mathrm{(b)}\,\,\,\,\,\vec{v}_I=(10\,\vec{\imath}-5\,\vec{\jmath}-\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 10 & -5 & -1 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0} & \,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \\ \\ \mathrm{(c)}\,\,\,\,\,\vec{v}_I=(12\,\vec{\imath}-\vec{\jmath}-6\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 12 & -1 & -6 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0} & \,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \\ \\ \mathrm{(d)}\,\,\,\,\,\vec{v}_I=(5\,\vec{\imath}-15\,\vec{\jmath}+5\,\vec{k}\,)\,\mathrm{m}/\mathrm{s} & \,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\times\vec{\omega}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 5 & -15 & 5 \\ 2 & -1 & 0 \end{array}\right|\neq\vec{0} & \,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_I\not\,\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,I\not\in \mathrm{EIRMD} \end{array}$

3 Segundo método: determinación del EIRMD

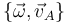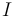Partiendo del conocimiento de la reducción cinemática $\{\vec{\omega},\vec{v}_A\}\,$ , es posible determinar el EIRMD del movimiento helicoidal instantáneo. En efecto: aplicando la ecuación vectorial del EIRMD, obtenemos la posición (relativa a $A\,$ ) de un punto genérico $I\,$ del EIRMD:

$\overrightarrow{AI}=\frac{\vec{\omega}\times\vec{v}_A}{|\,\vec{\omega}\,|^2}\,+\,\lambda\,\vec{\omega}=\frac{1}{5}\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -1 & 0 \\ 5 & -15 & 5 \end{array}\right|\,+\,\lambda\,(2\,\vec{\imath}\,-\,\vec{\jmath}\,)=[\,(-1\,+\,2\lambda)\,\vec{\imath}\,-\,(2\,+\,\lambda)\,\vec{\jmath}\,-\,5\,\vec{k}\,]\,\mathrm{m}$

Y conocidas las coordenadas del punto 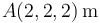$A(2,2,2)\,\mathrm{m}\,$ en el triedro OXYZ de referencia, es fácil determinar las coordenadas en dicho triedro de un punto genérico 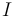$I\,$ del EIRMD:

$\left.\begin{array}{l} \overrightarrow{OA}=(2\,\vec{\imath}+2\,\vec{\jmath}+2\,\vec{k}\,)\,\mathrm{m} \\ \\ \overrightarrow{AI}=[\,(-1+2\lambda)\,\vec{\imath}\,-(2+\lambda)\,\vec{\jmath}\,-5\,\vec{k}\,]\,\mathrm{m} \end{array}\right\}\,\longrightarrow\,\,\,\overrightarrow{OI}=\overrightarrow{OA}\,+\,\overrightarrow{AI}=[\,(1+\,2\lambda)\,\vec{\imath}\,-\,\lambda\,\vec{\jmath}\,-\,3\,\vec{k}\,]\,\mathrm{m}\,\,\,\,\,\longrightarrow\,\,\,\,\, I(1+\,2\lambda,-\lambda,-3)\,\mathrm{m}$

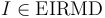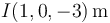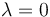Comparando esta terna $λ$ -paramétrica de coordenadas con las cuatro ternas propuestas en el enunciado, deducimos de inmediato que la única que corresponde a un punto $I\in\mathrm{EIRMD}\,$ es la de la respuesta (a), siendo concretamente $\,\,\,I(1,0,-3)\,\mathrm{m}\,$ el punto obtenido para $\lambda=0\,$ .