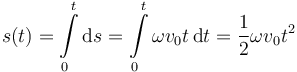Ejercicio de movimiento plano, Enero 2014 (F1 GIA)

De Laplace

Revisión a fecha de 10:52 20 ene 2015; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

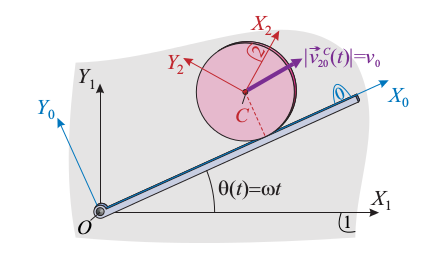
Una barra de longitud indefinida (sólido "0") se mueve siempre contenida en un plano fijo 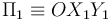$\Pi_1\equiv OX_1Y_1$ (sólido "1"). En el punto fijo $O$ del plano $Π 1$ está articulado uno de los extremos de la barra, la cuál se mueve de manera que el ángulo que forma con el eje $O X 1$ varía linealmente con el tiempo, según la ley horaria $θ(t) = ω t$ . Un disco de radio $R$ (sólido "2"), también siempre contenido en el plano $O X 1 Y 1$ , rueda sin deslizar sobre la barra "0". Respecto de un sistema de referencia $O X 0 Y 0$ solidario con la barra "0", el centro $C$ del disco realiza un movimiento rectilíneo uniforme de velocidad $v 0$ . En el instante inicial $(t = 0)$ , el centro del disco se halla en el eje $O Y 1$ .

Obtenga los elementos de la reducción cinemática del movimiento {21} y su derivada temporal.
Considérese el caso en que los parámetros del sistema verifican la relación $v 0 = ω R$ . ¿Qué tipo de movimiento realiza el disco respecto del plano fijo? Determine gráficamente, y de manera razonada, las posiciones de los C.I.R. correspondientes a los movimientos {01}, {20} y {21}.
También en el caso de $v 0 = ω R$ , calcule las componentes intrínsecas de la aceleración y la velocidad del centro $C$ del disco en movimiento {21}, en función del tiempo. Obtenga la ley horaria $s (t)$ para la distancia recorrida por el centro $C$ del disco, desde el instante inicial, sobre la trayectoria que dicho punto describe en el plano $Π 1$ .

2 Solución

2.1 Reducción del movimiento {21}

Vamos a usar la composición de movimientos {21} = {20} + {01}. Analicemos los dos movimientos mas simples.

2.1.1 Barra respecto del plano fijo {01}

Esta es la rotación de los ejes $O X 0 Y 0$ respecto del plano fijo. El eje $O X 0$ y el eje $O X 1$ forman el ángulo $θ$ , por lo que el vector rotación instantánea $\vec{\omega}_{01}$ es

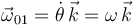
$\vec{\omega}_{01} = \dot{\theta}\,\vec{k} = \omega\,\vec{k}$

Por otro lado, la barra gira en torno al punto $O$ , por lo que este es el C.I.R. de este movimiento, es decir

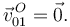
$\vec{v}^{\,O}_{01} = \vec{0}.$

Por tanto la reducción canónica de este movimiento es

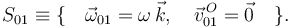
$S_{01} \equiv \{\quad \vec{\omega}_{01} = \omega\,\vec{k}, \quad \vec{v}^{\,O}_{01} = \vec{0} \quad\}.$

Calculamos su derivada. Como $ω$ es constante tenemos

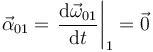
$\vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}$

Y además el punto $O$ siempre está en reposo, por lo que

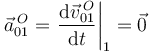
$\vec{a}^{\,O}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}$

2.1.2 Disco respecto de la barra {20}

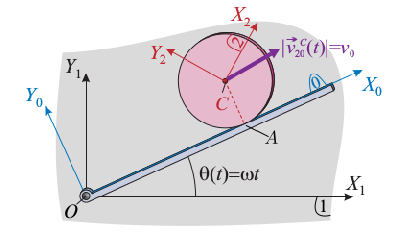
El enunciado nos da la velocidad del punto $C$ , y nos dice que el disco rueda sin deslizar sobre la barra, por lo que 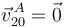$\vec{v}^{\,A}_{20}=\vec{0}$ , siendo $A$ el punto de contacto del disco con la barra. Al ser el movimiento plano sabemos que 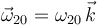$\vec{\omega}_{20} = \omega_{20}\,\vec{k}$ . Utilizamos el teorema de Chasles para encontrar el valor de $ω 20$ .

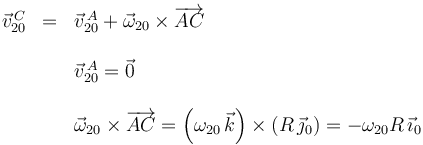
$\begin{array}{lcl} \vec{v}^{\,C}_{20} &=& \vec{v}^{\,A}_{20} + \vec{\omega}_{20}\times\overrightarrow{AC} \\ &&\\ && \vec{v}^{\,A}_{20} = \vec{0} \\ &&\\ && \vec{\omega}_{20}\times\overrightarrow{AC} = \left(\omega_{20}\,\vec{k}\right)\times\left(R\,\vec{\jmath}_0\right) =-\omega_{20}R\,\vec{\imath}_0 \end{array}$

Comparando con el valor del enunciado obtenemos la reducción cinemática del movimiento en el punto $C$

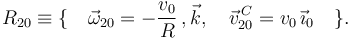
$R_{20} \equiv \{\quad \vec{\omega}_{20} = -\dfrac{v_0}{R}\,,\vec{k}, \quad \vec{v}^{\,C}_{20} = v_0\,\vec{\imath}_0 \quad\}.$

Calculamos su derivada temporal. Como $v 0$ es constante tenemos

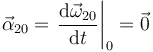
$\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}$

Y también

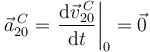
$\vec{a}^{\,C}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,C}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}$

2.1.3 Disco respecto al plano fijo {21}

Usamos las fórmulas de composición para obtener la reducción. Para el vector rotación tenemos

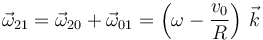
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = \left(\omega - \dfrac{v_0}{R}\right)\,\vec{k}$

Calculamos 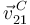$\vec{v}^{\,C}_{21}$

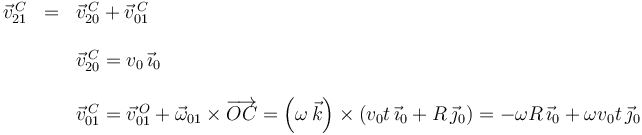
$\begin{array}{lcl} \vec{v}^{\,C}_{21} &=& \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} \\ &&\\ && \vec{v}^{\,C}_{20} = v_0\,\vec{\imath}_0 \\ &&\\ && \vec{v}^{\,C}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OC} = \left(\omega\,\vec{k}\right)\times\left(v_0t\,\vec{\imath}_0 + R\,\vec{\jmath}_0\right) = -\omega R\,\vec{\imath}_0 + \omega v_0t\,\vec{\jmath}_0 \end{array}$

Hemos usado que la distancia entre el punto $A$ y el punto $O$ es $v 0 t$ . La reducción cinemática en $C$ es

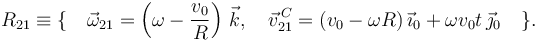
$R_{21} \equiv \{\quad \vec{\omega}_{21} = \left(\omega - \dfrac{v_0}{R}\right)\,\vec{k}, \quad \vec{v}^{\,C}_{21} = (v_0-\omega R)\,\vec{\imath}_0 + \omega v_0t\,\vec{\jmath}_0 \quad\}.$

Aplicamos las leyes de composición para calcular la derivada temporal

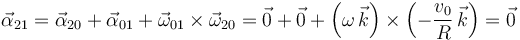
$\vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} = \vec{0} + \vec{0} + \left(\omega\,\vec{k}\right)\times\left(-\dfrac{v_0}{R}\,\vec{k}\right) = \vec{0}$

Y, finalmente

$\begin{array}{lcl} \vec{a}^{\,C}_{21} &=& \vec{a}^{\,C}_{20} + \vec{a}^{\,C}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,C}_{20} \\ &&\\ && \vec{a}^{\,C}_{20} = \vec{0} \\ &&\\ && \vec{a}^{\,C}_{01} = \vec{a}^{\,O}_{01} + \vec{\alpha}_{01}\times\overrightarrow{OC} - \omega_{01}^2\overrightarrow{OC} = -\omega^2\,\left(v_0t\,\vec{\imath}_0 + R\,\vec{\jmath}_0\right) \\ &&\\ && 2\vec{\omega}_{01}\times\vec{v}^{\,C}_{20} = 2\,\left(\omega\,\vec{k}\right)\times(v_0\,\vec{\imath}_0) = 2\omega v_0\,\vec{\jmath}_0 \end{array}$

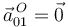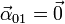Hemos usado que $\vec{a}^{\,O}_{01}=\vec{0}$ y $\vec{\alpha}_{01}=\vec{0}$ . Finalmente obtenemos

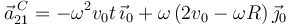
$\vec{a}^{\,C}_{21} = -\omega^2v_0t\,\vec{\imath}_0 + \omega\,(2v_0 - \omega R)\,\vec{\jmath}_0$

2.2 Localización de los CIRs en el caso $v 0 = ω R$

Si los valores de los parámetros son tales que $v 0 = ω R$ , el vector rotación $\vec{\omega}_{21}$ se anula. Por tanto, el disco realiza una traslación respecto al plano fijo, con una velocidad

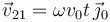
$\vec{v}_{21} = \omega v_0t\,\vec{\jmath}_0$

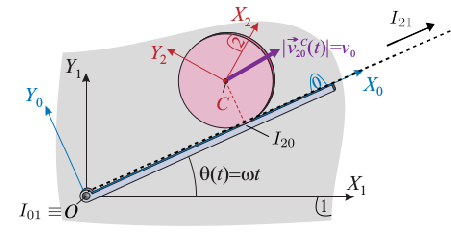
Recordemos que en el caso de una traslación no es necesario poner la letra com superíndice en la velocidad, pues todos los puntos tienen la misma velocidad. La figura muestra los C.I.R. de los tres movimientos. El punto $O$ es el $I 01$ . El punto de contacto entre el disco y la barra es el $I 20$ . Por el teorema de los tres centros, el $I 21$ debe estar en la línea que une $I 01$ y $I 20$ . Y al tratarse de una traslación, se localiza en el infinito.

2.3 Componentes intrínsecas en el movimiento {21} del punto $C$

Para los valores de los parámetros indicados en el enunciado tenemos

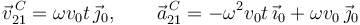
$\vec{v}_{21}^{\,C} = \omega v_0t\,\vec{\jmath}_0, \qquad \vec{a}_{21}^{\,C} = -\omega^2 v_0t\,\vec{\imath}_0 + \omega v_0\,\vec{\jmath}_0$

Obtenemos el vector tangente a partir del vector velocidad

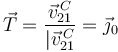
$\vec{T} = \dfrac{\vec{v}_{21}^{\,C}}{|\vec{v}_{21}^{\,C}} = \vec{\jmath}_0$

La componente intrínseca de la velocidad es tal que 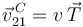$\vec{v}_{21}^{\,C}=v\,\vec{T}$ , por tanto

$v = ω v 0 t$

La componente tangencial de la aceleración es

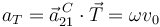
$a_T = \vec{a}_{21}^{\,C}\cdot\vec{T} = \omega v_0$

y la normal es

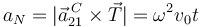
$a_N = |\vec{a}_{21}^{\,C}\times\vec{T}| = \omega^2v_0t$

Obtenemos la distancia recorrida integrando el desplazamiento infinitesimal

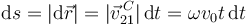
$\mathrm{d}s = |\mathrm{d}\vec{r}| = |\vec{v}^{\,C}_{21}|\,\mathrm{d}t = \omega v_0 t\,\mathrm{d}t$

Para un instante arbitrario tenemos

$s(t) = \int\limits_0^t\mathrm{d}s = \int\limits_0^t \omega v_0 t\,\mathrm{d}t = \dfrac{1}{2}\omega v_0 t^2$

Ejercicio de movimiento plano, Enero 2014 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción del movimiento {21}

2.1.1 Barra respecto del plano fijo {01}

2.1.2 Disco respecto de la barra {20}

2.1.3 Disco respecto al plano fijo {21}

2.2 Localización de los CIRs en el caso $v 0 = ω R$

2.3 Componentes intrínsecas en el movimiento {21} del punto $C$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Ejercicio de movimiento plano, Enero 2014 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción del movimiento {21}

2.1.1 Barra respecto del plano fijo {01}

2.1.2 Disco respecto de la barra {20}

2.1.3 Disco respecto al plano fijo {21}

2.2 Localización de los CIRs en el caso v0 = ωR

2.3 Componentes intrínsecas en el movimiento {21} del punto C

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Localización de los CIRs en el caso $v 0 = ω R$

2.3 Componentes intrínsecas en el movimiento {21} del punto $C$