Entrar Página Discusión Historial Go to the site toolbox

Centro de masas de diversos sistemas continuos (GIC)

De Laplace

Contenido

1 Enunciado

Calcula la posición del centro de masas de los siguientes sistemas continuos

  1. Una varilla de longitud L con densidad de masa constante.
  2. Una varilla de longitud L y masa M, con densidad de masa 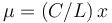\mu = (C/L)\,x (el punto x = 0 corresponde a un extremo de la varilla)
  3. Un aro semicircular de masa M y radio R.
  4. Dos esferas macizas de masas M1 y M2 y radios R y 2R, unidas por un cilindro de masa M3 y longitud L.

2 Solución

2.1 Introducción teórica

Para un sistema de N masas puntuales, cada una con masa mi y vector de posición 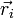\vec{r}_i , la posición del centro de masas viene dada por la expresión

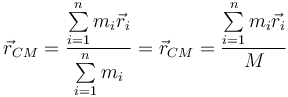
\vec{r}_{CM} = \dfrac{\sum\limits_{i=1}^nm_i\vec{r}_i}{\sum\limits_{i=1}^nm_i} = \vec{r}_{CM} = \dfrac{\sum\limits_{i=1}^nm_i\vec{r}_i}{ M}

El denominador es la masa total del sistema.

La técnica para calcular centros de masas en sistemas continuos consiste en dividirlos en pequeñas masas (diferenciales de masa dm) y aplicar a éstas la fórmula anterior. Al hacer esto, aplicamos las transformaciones

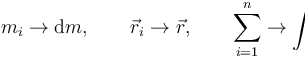
m_i \to \mathrm{d}m, \qquad \vec{r}_i\to\vec{r}, \qquad \sum\limits_{i=1}^n \to \int

y la posición del centro de masas se convierte en

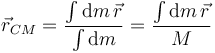
\vec{r}_{CM} = \dfrac{\int\mathrm{d}m\,\vec{r}}{\int\mathrm{d}m} = \dfrac{\int\mathrm{d}m\,\vec{r}}{M}

La integral se extiende a todo el volumen del sólido.

2.2 Varilla homogénea

Obtenido de "http://tesla.us.es/wiki/index.php/Centro_de_masas_de_diversos_sistemas_continuos_(GIC)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace