Centro de masas de diversos sistemas continuos (GIC)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Calcula la posición del centro de masas de los siguientes sistemas continuos

Una varilla de longitud $L$ con densidad de masa constante.
Una varilla de longitud $L$ y masa $M$ , con densidad de masa 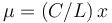$\mu = (C/L)\,x$ (el punto $x = 0$ corresponde a un extremo de la varilla)
Un aro semicircular de masa $M$ y radio $R$ .
Dos esferas macizas de masas $M 1$ y $M 2$ y radios $R$ y $2 R$ , unidas por un cilindro de masa $M 3$ y longitud $L$ .

2 Solución

2.1 Introducción teórica

Para un sistema de n masas puntuales, cada una con masa $m i$ y vector de posición 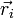$\vec{r}_i$ , la posición del centro de masas viene dada por la expresión

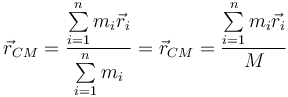
$\vec{r}_{CM} = \dfrac{\sum\limits_{i=1}^nm_i\vec{r}_i}{\sum\limits_{i=1}^nm_i} = \vec{r}_{CM} = \dfrac{\sum\limits_{i=1}^nm_i\vec{r}_i}{ M}$

El denominador es la masa total del sistema.

La técnica para calcular centros de masas en sistemas continuos consiste en dividirlos en pequeñas masas (diferenciales de masa $d m$ ) y aplicar a éstas la fórmula anterior. Al hacer esto, aplicamos las transformaciones

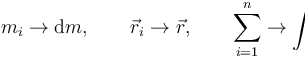
$m_i \to \mathrm{d}m, \qquad \vec{r}_i\to\vec{r}, \qquad \sum\limits_{i=1}^n \to \int$

y la posición del centro de masas se convierte en

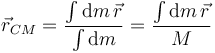
$\vec{r}_{CM} = \dfrac{\int\mathrm{d}m\,\vec{r}}{\int\mathrm{d}m} = \dfrac{\int\mathrm{d}m\,\vec{r}}{M}$

La integral se extiende a todo el volumen del sólido.

2.2 Varilla homogénea

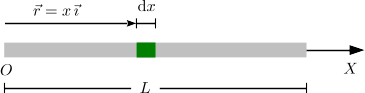
Dividimos la varilla en pequeños trozos de masa $d m$ . Queremos calcular la posición del centro de masas respecto al punto $O$ . Como se indica en la figura, la posición de cada masa diferencial puede expresarse como

$\vec{r} = x\,\vec{\imath} \qquad\qquad 0\leq x \leq L$

La longitud de cada trocito puede escribirse como

$d l = d x$

Podemos expresar la masa de cada trocito en función de la densidad lineal de masa. Para una varilla homogénea la densidad lineal de masa es la misma en todos sus puntos y vale

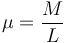
$\mu = \dfrac{M}{L}$

Entonces, la masa de un trocito es la densidad lineal de masa por su longitud

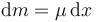
$\mathrm{d}m = \mu\,\mathrm{d}x$

Entonces la integral que aparece en el numerador de la expresión para calcular el centro de masas es

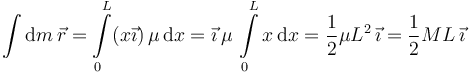
$\int\mathrm{d}m\,\vec{r} = \int\limits_0^L (x\vec{\imath})\,\mu\,\mathrm{d}x = \vec{\imath}\,\mu\,\int\limits_0^L x\,\mathrm{d}x = \dfrac{1}{2}\mu L^2\,\vec{\imath} = \dfrac{1}{2}ML\,\vec{\imath}$

Hemos usado que $μ$ y $\vec{\imath}$ no dependen de $x$ y salen de la integral. Además, hemos utilizado que $μ = M / L$ .

Entonces, el vector de posición del centro de masas es

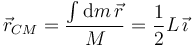
$\vec{r}_{CM} = \dfrac{\int\mathrm{d}m\,\vec{r}}{M} = \dfrac{1}{2}L\,\vec{\imath}$

El CM está en el centro de la varilla, como se puede deducir por argumentos de simetría pues la varilla es homogénea.

2.3 Varilla con densidad de masa variable

Ahora nos dan como dato la densidad lineal de masa de la varilla

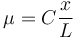
$\mu = C\dfrac{x}{L}$

siendo $C$ una constante. Esto quiere decir que la densidad aumenta cuando nos desplazamos hacia la derecha de la varilla.

Ahora tenemos que calcular la masa de la varilla sumando las masas de todos los trocitos. La masa de cada uno es

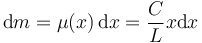
$\mathrm{d}m = \mu(x)\,\mathrm{d}x = \dfrac{C}{L}x\mathrm{d}x$

La masa total es la suma de todos ellos, es decir, la integral

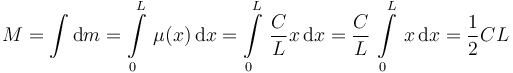
$M = \int\mathrm{d}m = \int\limits_0^L\,\mu(x)\,\mathrm{d}x = \int\limits_0^L \,\dfrac{C}{L}x\,\mathrm{d}x = \dfrac{C}{L}\,\int\limits_0^L\,x\,\mathrm{d}x = \dfrac{1}{2}CL$

La otra integral que necesitamos es

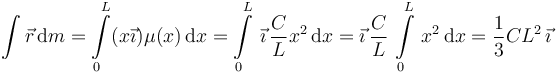
$\int\vec{r}\,\mathrm{d}m = \int\limits_0^L (x\vec{\imath})\mu(x)\,\mathrm{d}x = \int\limits_0^L\,\vec{\imath}\, \dfrac{C}{L} x^2\,\mathrm{d}x = \vec{\imath}\, \dfrac{C}{L}\,\int\limits_0^L\, x^2\,\mathrm{d}x = \dfrac{1}{3}CL^2\,\vec{\imath}$

Por tanto, la posición del centro de masas es

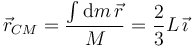
$\vec{r}_{CM} = \dfrac{\int\mathrm{d}m\,\vec{r}}{M} = \dfrac{2}{3}L\,\vec{\imath}$

Ahora el CM está desplazado hacia la derecha, pues la densidad de la varilla aumenta en esa dirección.

2.4 Varilla semicircular

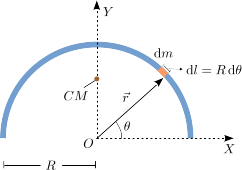
Consideramos ahora la varilla homogénea semicircular de la figura, de masa $M$ y radio $R$ . De nuevo la dividimos en pequeños trozos diferenciales de masa. Podemos parametrizar la posición de cada trozo utilizando el ángulo $θ$ de la figura

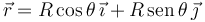
$\vec{r} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}$

Al ser homogénea la densidad de masa se puede calcular dividiendo su masa por su longitud

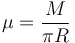
$\mu = \dfrac{M}{\pi R}$

La longitud de cada trocito es

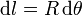
$\mathrm{d}l = R\,\mathrm{d}\theta$

Este resultado se puede obtener razonando que cuando el arco es muy pequeño, su longitud es igual a la de la cuerda. También podemos decir que, para obtener un pequeño desplazamiento, hemos de mover la punta del vector un pequeño $dθ$ . La distancia recorrida en ese desplazamiento es

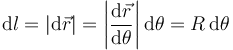
$\mathrm{d}l = |\mathrm{d}\vec{r}| = \left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|\mathrm{d}\theta = R\,\mathrm{d}\theta$

Ahora podemos calcular la integral vectorial para calcular la posición del centro de masas

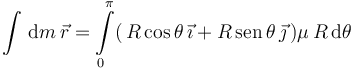
$\int\,\mathrm{d}m \,\vec{r} = \int\limits_0^{\pi}(\,R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}\,) \mu\,R\,\mathrm{d}\theta$

La integral de la suma es la suma de las integrales. También tenemos en cuenta que los vectores cartesianos $\vec{\imath}$ y $\vec{\jmath}$ no dependen de $θ$ , como tampoco lo hacen $R$ y $μ$ . Todos estos valores salen de las integrales, y nos queda

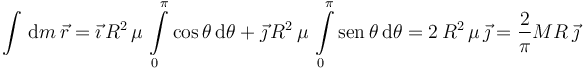
$\int\,\mathrm{d}m \,\vec{r} = \vec{\imath}\,R^2\,\mu\,\int\limits_0^{\pi}\cos\theta\,\mathrm{d}\theta + \vec{\jmath}\, R^2\,\mu\,\int\limits_0^{\pi}\mathrm{sen}\,\theta\,\mathrm{d}\theta = 2\,R^2\,\mu\,\vec{\jmath} = \dfrac{2}{\pi}MR\,\vec{\jmath}$

El centro de masas está entonces en

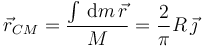
$\vec{r}_{CM} = \dfrac{\int\,\mathrm{d}m \,\vec{r}}{M} = \dfrac{2}{\pi}R\,\vec{\jmath}$

En la figura se indica la posición del CM. Vemos que está en el eje $Y$ . Esto es correcto, pues esa línea es un eje de simetría del semiaro, y el CM tiene que estar en los elementos de simetría. Por otro lado, también observamos que el CM está fuera del aro. En efecto, el CM no tiene por qué está dentro del cuerpo.

Este semiaro sirve para modelar un saltador de altura cuando pasa sobre el listón. Al saltar hacia atrás arqueando el cuerpo consigue que el CM pase por debajo del listón. Está técnica de salto permite alcanzar alturas mayores con la misma energía de batida.

Centro de masas de diversos sistemas continuos (GIC)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Introducción teórica

2.2 Varilla homogénea

2.3 Varilla con densidad de masa variable

2.4 Varilla semicircular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES