Base vectorial girada

De Laplace

Revisión a fecha de 23:35 2 oct 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Base ortonormal dextrógira
- 2.1 Base ortonormal
- 2.2 Base dextrogira
3 Transformación inversa
4 caso particular

1 Enunciado

Considere la terna de vectores

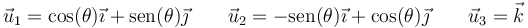
$\vec{u}_1 = \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \qquad \vec{u}_2 = -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \qquad \vec{u}_3 = \vec{k}$

Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
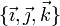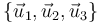Halle la transformación inversa, es decir, exprese $\{\vec{\imath},\vec{\jmath},\vec{k}\}$ como combinación de $\{\vec{u}_1,\vec{u}_2,\vec{u}_3\}$ .
Para el caso particular en que $tg(θ) = 3 / 4$ , particularice las ecuaciones de transformación y exprese el vector 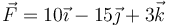$\vec{F}=10\vec{\imath}-15\vec{\jmath}+3\vec{k}$ en la nueva base.

2 Base ortonormal dextrógira

2.1 Base ortonormal

Para demostrar que se tra de una base ortonormal hay que probar que son unitarios y ortogonales entre sí, es decir

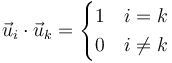
$\vec{u}_i\cdot\vec{u}_k=\begin{cases}1 & i = k \\ 0 & i\neq k\end{cases}$

Calculamos entonces los productos escalares:

De 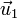$\vec{u}_1$ consigo mismo

$\vec{u}_1\cdot\vec{u}_1=\cos^2(\theta)+\mathrm{sen}^2(\theta) = 1$

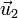De $\vec{u}_1$ con $\vec{u}_2$ (y viceversa, por la conmutatividad)

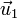$\vec{u}_1\cdot\vec{u}_2=\vec{u}_2\cdot\vec{u}_1=\cos(\theta)(-\mathrm{sen}(theta))+\mathrm{sen}(\theta)\cos(\theta) = 0$

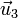De $\vec{u}_1$ con $\vec{u}_3$ (y viceversa). Es fácil ver que son ortogonales ya que 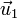$\vec{u}_1$ no tiene componente en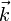 $\vec{k}$

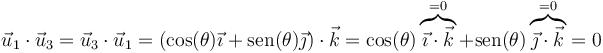
$\vec{u}_1\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_1=(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})\cdot\vec{k}= \cos(\theta)\overbrace{\vec{\imath}\cdot\vec{k}}^{=0}+\mathrm{sen}(\theta)\overbrace{\vec{\jmath}\cdot\vec{k}}^{=0} = 0$

De 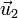$\vec{u}_2$ consigo mismo

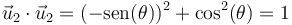
$\vec{u}_2\cdot\vec{u}_2=(-\mathrm{sen}(\theta))^2+\cos^2(\theta) = 1$

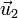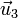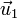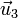
De $\vec{u}_2$ con $\vec{u}_3$ (y viceversa). Se anula el producto escalar por la misma razón que el de $\vec{u}_1$ con $\vec{u}_3$

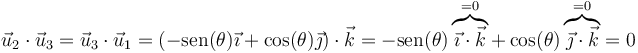
$\vec{u}_2\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_1=(-\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath})\cdot\vec{k}= -\mathrm{sen}(\theta)\overbrace{\vec{\imath}\cdot\vec{k}}^{=0}+\cos(\theta)\overbrace{\vec{\jmath}\cdot\vec{k}}^{=0} = 0$

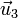De $\vec{u}_3$ consigo mismo

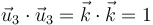
$\vec{u}_3\cdot\vec{u}_3=\vec{k}\cdot\vec{k} = 1$

Por tanto, hemos demostrado que la relación anterior para los productos escalares se cumple y la base es ortonormal.

2.2 Base dextrogira

Para demostrar que se trata de una base dextrógira hemos de probar que se cumple la regla de la mano derecha, es decir, que

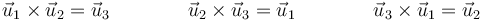
$\vec{u}_1\times\vec{u}_2=\vec{u}_3\qquad \qquad \vec{u}_2\times\vec{u}_3=\vec{u}_1\qquad \qquad \vec{u}_3\times\vec{u}_1=\vec{u}_2$

Probamos la primera de las igualdades

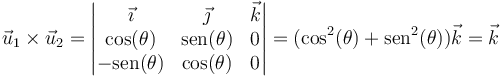
$\vec{u}_1\times\vec{u}_2=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \cos(\theta) & \mathrm{sen}(\theta) & 0 \\ -\mathrm{sen}(\theta) & \cos(\theta) & 0\end{matrix}\right|=(\cos^2(\theta)+\mathrm{sen}^2(\theta))\vec{k}=\vec{k}$

De la misma manera se demuestran las otras dos igualdades. Una forma alternativa de demostrarlas es observar que

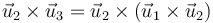
$\vec{u}_2\times\vec{u}_3 = \vec{u}_2\times(\vec{u}_1\times\vec{u}_2)$

Aplicamos las propiedades del doble producto vectorial

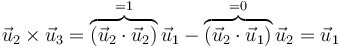
$\vec{u}_2\times\vec{u}_3 = \overbrace{(\vec{u}_2\cdot \vec{u}_2)}^{=1}\vec{u}_1-\overbrace{(\vec{u}_2\cdot \vec{u}_1)}^{=0}\vec{u}_2=\vec{u}_1$

y de la misma manera se obtiene la tercera

$\vec{u}_3\times\vec{u}_1=\vec{u}_2$

por lo que la base es ortonormal y dextrógira.

3 Transformación inversa

4 caso particular

Base vectorial girada

De Laplace

Contenido

1 Enunciado

2 Base ortonormal dextrógira

2.1 Base ortonormal

2.2 Base dextrogira

3 Transformación inversa

4 caso particular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES