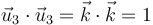Entrar Página Discusión Historial Go to the site toolbox

Base vectorial girada

De Laplace

Contenido

1 Enunciado

Considere la terna de vectores

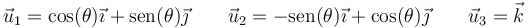
\vec{u}_1 = \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \qquad \vec{u}_2 = -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \qquad \vec{u}_3 = \vec{k}
  1. Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
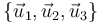  2. Halle la transformación inversa, es decir, exprese \{\vec{\imath},\vec{\jmath},\vec{k}\} como combinación de \{\vec{u}_1,\vec{u}_2,\vec{u}_3\}.
  3. Para el caso particular en que tg(θ) = 3 / 4, particularice las ecuaciones de transformación y exprese el vector 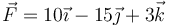\vec{F}=10\vec{\imath}-15\vec{\jmath}+3\vec{k} en la nueva base.

2 Base ortonormal dextrógira

2.1 Base ortonormal

Para demostrar que se tra de una base ortonormal hay que probar que son unitarios y ortogonales entre sí, es decir

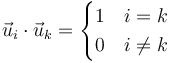
\vec{u}_i\cdot\vec{u}_k=\begin{cases}1 & i = k \\ 0 & i\neq k\end{cases}

Calculamos entonces los productos escalares:

  • De 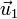\vec{u}_1 consigo mismo
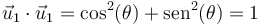
\vec{u}_1\cdot\vec{u}_1=\cos^2(\theta)+\mathrm{sen}^2(\theta) = 1
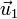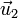  • De \vec{u}_1 con \vec{u}_2 (y viceversa, por la conmutatividad)
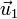\vec{u}_1\cdot\vec{u}_2=\vec{u}_2\cdot\vec{u}_1=\cos(\theta)(-\mathrm{sen}(theta))+\mathrm{sen}(\theta)\cos(\theta) = 0
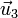  • De \vec{u}_1 con \vec{u}_3 (y viceversa). Es fácil ver que son ortogonales ya que 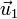\vec{u}_1 no tiene componente en \vec{k}
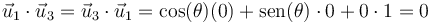
\vec{u}_1\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_1=\cos(\theta)(0)+\mathrm{sen}(\theta)\cdot 0 +0\cdot 1 = 0
  • De 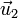\vec{u}_2 consigo mismo
\vec{u}_2\cdot\vec{u}_2=(-\mathrm{sen}(\theta))^2+\cos^2(\theta) = 1
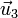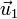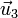
  • De \vec{u}_2 con \vec{u}_3 (y viceversa). Se anula el producto escalar por la misma razón que el de \vec{u}_1 con \vec{u}_3
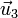\vec{u}_2\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_2=-\mathrm{sen}(\theta)(0)+\cos(\theta)\cdot 0 +0\cdot 1 = 0
  • De \vec{u}_3 consigo mismo
\vec{u}_3\cdot\vec{u}_3=\vec{k}\cdot\vec{k} = 1


3 Transformación inversa

4 caso particular

Obtenido de "http://tesla.us.es/wiki/index.php/Base_vectorial_girada"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace