Dos masas en planos inclinados y un muelle
De Laplace
Revisión a fecha de 21:38 10 sep 2014; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Dos masas iguales de peso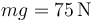 
situadas sobre dos planos inclinados contiguos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.
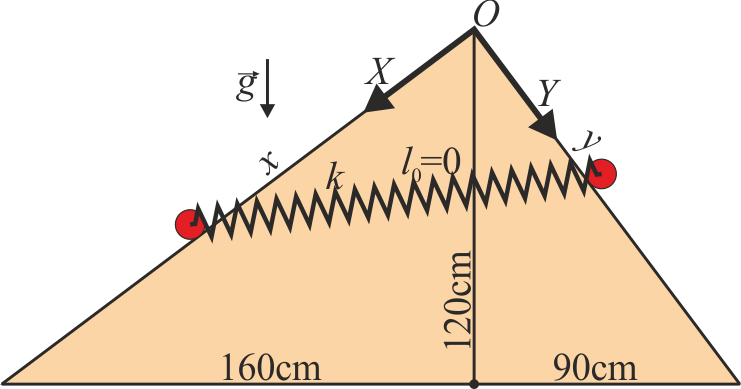
Las masas están unidas por un resorte ideal de longitud natural nula y constante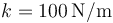 
. No hay rozamiento con las superficies.
- Determine la posición de equilibrio de las dos masas, hallando los valores de x e y.
- Para esta posición de equilibrio, calcule las fuerzas de reacción ejercidas por los planos, así como la fuerza elástica que el resorte ejerce sobre cada masa.
- Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre las masas y las superficies en que se apoyan. En ese caso hay un rango de posiciones en las que puede producirse el equilibrio. ¿Cuánto valen x e y para la posición de equilibrio con mínima longitud del resorte? ¿Y para el caso de máxima longitud del resorte?
Sugerencia: Empléense los ejes de la figura.
2 Posición de equilibrio
Por estar en equilibrio, la suma de las fuerzas sobre cada masa debe anularse.
Si llamamos masa “1” a la de la izquierda tenemos que las fuerzas que actúan sobre ella son:
- Peso
- que en los ejes indicados valen
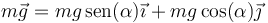
- con
- lo que da el valor numérico
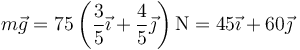
- Fuerza elástica
- Cuando la longitud natural de un resorte es nula, la fuerza elástica que produce la da la ley de Hooke vectorial
- siendo
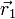el vector que va desde el otro extremo del muelle hasta el que ocupa la partícula 1. En este caso sería
- y por tanto
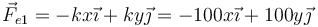
- Reacción normal del plano: Esta es perpendicular al plano y va en el sentido hacia afuera
Sumando las tres fuerzas
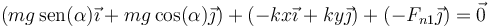
y separando en componentes
