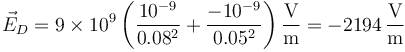Dos esferas huecas

De Laplace

1 Enunciado

Se tiene un sistema de cargas formado por dos superficies esféricas de radio 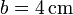cuyos centros distan 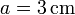, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de 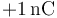y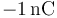

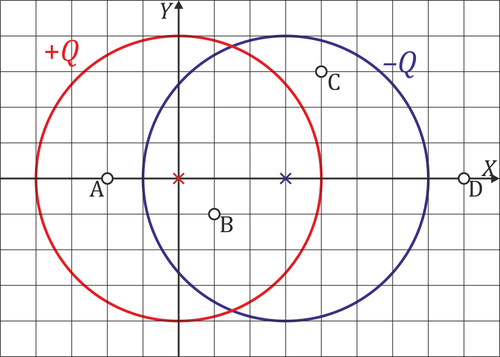
Para los puntos marcados en la figura (en cm)

1. Calcule el campo eléctrico.
2. Calcule el potencial eléctrico.
3. A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de 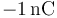desde el punto A al punto D moviéndola a lo largo del eje X.

2 Campo eléctrico

La solución de este problema es una simple aplicación del principio de superposición. Basta con hallar el campo de cada superficie esférica y luego sumar las dos contribuciones.

El campo debido a una superficie esférica de radio acargada uniformemente tiene la expresión

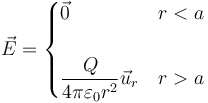
siendo r las distancia del punto de observación al centro de la esfera y 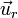el vector unitario radial hacia afuera.

Así, tenemos para los cuatro puntos lo siguiente:

Punto A

Este punto está dentro de la esfera de carga positiva y fuera de la negativa. Para esta última la distancia al centro es de 5 cm y el vector unitario radial es 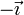. Por tanto

Punto B

Se encuentra en el interior de las dos esferas, por lo que

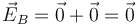
Punto C

Éste se halla dentro de la esfera de carga negativa y fuera de la positiva. La distancia al centro de esta es también de 5 cm, pero el unitario radial es ahora el que va en la dirección y sentido del vector

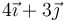
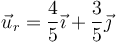
lo que da el campo

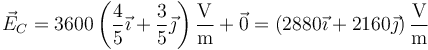
Punto D

Por último, este punto se encuentra fuera de las dos esferas, a 8 cm del centro de la esfera positiva y 5 de la negativa. El unitario radial es, en los dos casos 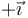, lo que nos da

3 Potencial eléctrico

4 Trabajo