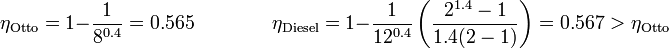Ciclo Diesel (GIE)

De Laplace

Revisión a fecha de 19:17 2 abr 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Rendimiento en función de las temperaturas
4 Rendimiento en función de los volúmenes
5 Caso práctico
6 Comparación con el ciclo Otto

1 Enunciado

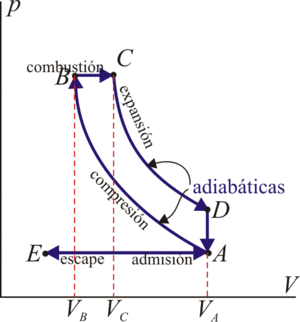
Un motor diésel puede modelarse con el ciclo ideal formado por seis pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión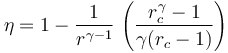 $\eta = 1 -\frac{1}{r^{\gamma-1}}\,\left(\frac{r_c^\gamma-1}{\gamma(r_c-1)}\right)$

siendo $r = V A / V B$ la razón de compresión y $r c = V C / V B$ la relación de combustión. El método para obtener este resultado es análogo al empleado para el ciclo Otto. Compare los rendimientos del ciclo de Otto y el diésel. ¿Cuáles son las ventajas e inconvenientes respectivos?

2 Introducción

Un ciclo Diésel ideal es un modelo simplificado de lo que ocurre en un motor diésel. En un motor de esta clase, a diferencia de lo que ocurre en un motor de gasolina la combustión no se produce por la ignición de una chispa en el interior de la cámara. En su lugar, aprovechando las propiedades químicas del gasóleo, el aire es comprimido hasta una temperatura superior a la de autoignición del gasóleo y el combustible es inyectado a presión en este aire caliente, produciéndose la combustión de la mezcla.

Puesto que sólo se comprime aire, la relación de compresión (cociente entre el volumen en el punto más bajo y el más alto del pistón) puede ser mucho más alta que la de un motor de gasolina (que tiene un límite, por ser indeseable la autoignición de la mezcla). La relación de compresión de un motor diésel puede oscilar entre 12 y 24, mientras que el de gasolina puede rondar un valor de 8.

Para modelar el comportamiento del motor diésel se considera un ciclo Diesel de seis pasos, dos de los cuales se anulan mutuamente:

Admisión E→A: El pistón baja con la válvula de admisión abierta, aumentando la cantidad de aire en la cámara. Esto se modela como una expansión a presión constante (ya que al estar la válvula abierta la presión es igual a la exterior). En el diagrama PV aparece como una recta horizontal.
Compresión A→B: El pistón sube comprimiendo el aire. Dada la velocidad del proceso se supone que el aire no tiene posibilidad de intercambiar calor con el ambiente, por lo que el proceso es adiabático. Se modela como la curva adiabática reversible A→B, aunque en realidad no lo es por la presencia de factores irreversibles como la fricción. El punto inicial de esta curva es aquél en el que el pistón se halla lo más bajo posible. A este punto se le conoce como PMI (punto muerto inferior, BDC en inglés). El punto final corresponde a que el pistón esté en el punto más alto. Este es el PMS (punto muerto superior, TDC en inglés).
Combustión B→C: Un poco antes de que el pistón llegue a su punto más alto y continuando hasta un poco después de que empiece a bajar, el inyector introduce el combustible en la cámara. Al ser de mayor duración que la combustión en el ciclo Otto, este paso se modela como una adición de calor a presión constante. Éste es el único paso en el que el ciclo Diesel se diferencia del Otto.
Expansión C→D: La alta temperatura del gas empuja al pistón hacia abajo, realizando trabajo sobre él. De nuevo, por ser un proceso muy rápido se aproxima por una curva adiabática reversible.
Escape D→A y A→E: Se abre la válvula de escape y el gas sale al exterior, empujado por el pistón a una temperatura mayor que la inicial, siendo sustituido por la misma cantidad de mezcla fría en la siguiente admisión. El sistema es realmente abierto, pues intercambia masa con el exterior. No obstante, dado que la cantidad de aire que sale y la que entra es la misma podemos, para el balance energético, suponer que es el mismo aire, que se ha enfriado. Este enfriamiento ocurre en dos fases. Cuando el pistón está en su punto más bajo, el volumen permanece aproximadamente constante y tenemos la isócora D→A. Cuando el pistón empuja el aire hacia el exterior, con la válvula abierta, empleamos la isobara A→E, cerrando el ciclo.

En total, el ciclo se compone de dos subidas y dos bajadas del pistón, razón por la que es un ciclo de cuatro tiempos, aunque este nombre se suele reservar para los motores de gasolina.

3 Rendimiento en función de las temperaturas

Un ciclo diésel contiene dos proceso adiabáticos, A→B y C→D, en los que no se intercambia calor. De los otros dos, en el calentamiento a presión constante B→C, el gas recibe una cantidad de calor $Q in$ del exterior igual a

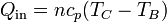
$Q_\mathrm{in} = nc_p(T_C-T_B)\,$

En el enfriamiento a volumen constante D→A el sistema cede una cantidad de calor al ambiente

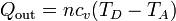
$Q_\mathrm{out} = nc_v(T_D-T_A)\,$

El rendimiento del ciclo será entonces

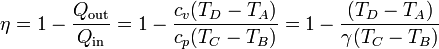
$\eta = 1 - \frac{Q_\mathrm{out}}{Q_\mathrm{in}} = 1 - \frac{c_v(T_D-T_A)}{c_p(T_C-T_B)}=1 - \frac{(T_D-T_A)}{\gamma(T_C-T_B)}$

con $γ = c p / c v$ la proporción entre las capacidades caloríficas.

4 Rendimiento en función de los volúmenes

La expresión anterior requiere conocer las cuatro temperaturas de los vértices del ciclo. Puede simplificarse teniendo en cuenta las características de cada uno de los procesos que lo componen.

Así tenemos, para la compresión adiabática A→B

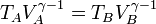
$T_AV_A^{\gamma-1} = T_BV_B^{\gamma-1}$

que, teniendo en cuenta la relación de compresión, podemos reescribir como

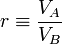
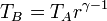
$r \equiv \frac{V_A}{V_B}$ $\Rightarrow$ $T_B = T_A r^{\gamma-1}\,$

Para la expansión a presión constante, aplicando la ecuación de estado de los gases ideales

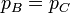
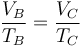
$p_B = p_C\,$ $\Rightarrow$ $\frac{V_B}{T_B} = \frac{V_C}{T_C}$

Introduciendo ahora la relación $r c = V C / V B$ obtenemos

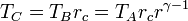
$T_C = T_Br_c = T_Ar_cr^{\gamma-1}\,$

Por último, para la temperatura en D aplicamos de nuevo la ley de Poisson y el que el enfriamiento es a volumen constante:

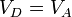
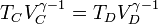
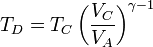
$V_D = V_A\,$ $T_CV_C^{\gamma-1}=T_DV_D^{\gamma-1}\,$ $\Rightarrow$ $T_D = T_C\left(\frac{V_C}{V_A}\right)^{\gamma-1}$

Multiplicando y dividiendo por $V B$ y aplicando el valor de la temperatura en C

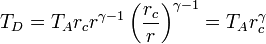
$T_D = T_Ar_cr^{\gamma-1}\left(\frac{r_c}{r}\right)^{\gamma-1}=T_Ar_c^\gamma$

Combinado estos resultados nos queda

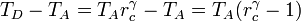
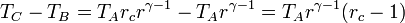
$T_D - T_A = T_Ar_c^\gamma-T_A = T_A(r_c^\gamma-1)\,$ $T_C-T_B = T_Ar_cr^{\gamma-1} - T_A r^{\gamma-1} = T_Ar^{\gamma-1}(r_c-1)\,$

Sustituyendo esto en la expresión del rendimiento obtenemos finalmente

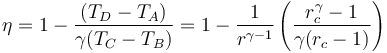
$\eta = 1 - \frac{(T_D-T_A)}{\gamma(T_C-T_B)}= 1 - \frac{1}{r^{\gamma-1}}\left(\frac{r_c^\gamma-1}{\gamma(r_c-1)}\right)$

5 Caso práctico

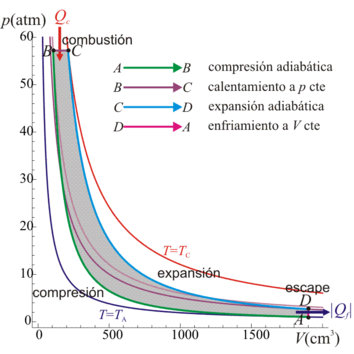
Vamos a considerar un ciclo Diesel en la que el aire a la entrada está a una presión de 1 atm y una temperatura de 17°C; la razón de compresión es 18 y la de combustión vale 2. El volumen máximo de la cámara es de 1900 cm³. Vamos a determinar los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor.

5.1 Estado inicial

Como punto de partida del ciclo de cuatro pasos tenemos que el gas a temperatura y presión ambientes llena el cilindro

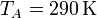
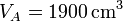
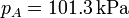
$T_A = 290\,\mathrm{K}$ $V_A = 1900\,\mathrm{cm}^3$ $p_A=101.3\,\mathrm{kPa}$

El número de moles contenidos en el cilindro es

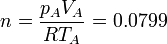
$n = \frac{p_AV_A}{RT_A}=0.0799$

5.2 Compresión adiabática

Tras la compresión, el volumen del cilindro se reduce según la razón de compresión

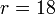
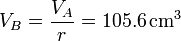
$r = 18\,$ $\Rightarrow$ $V_B = \frac{V_A}{r}=105.6\,\mathrm{cm}^3$

La temperatura al final la compresión la obtenemos de la ley de Poisson

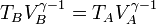
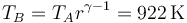
$T_BV_B^{\gamma-1} = T_AV_A^{\gamma-1}\,$ $\Rightarrow$ $T_B = T_A r^{\gamma-1}=922\,\mathrm{K}$

y la presión en este punto la hallamos mediante la ley de los gases ideales

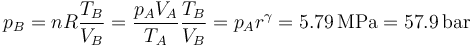
$p_B = nR\frac{T_B}{V_B} = \frac{p_AV_A}{T_A}\frac{T_B}{V_B}=p_Ar^\gamma = 5.79\,\mathrm{MPa}=57.9\,\mathrm{bar}$

5.3 Expansión isóbara

En el proceso de calentamiento, la presión se mantiene constante, por lo que

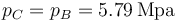
$p_C=p_B=5.79\,\mathrm{Mpa}$

mientras que el volumen lo da la relación de combustión

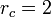
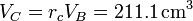
$r_c = 2\,$ $\Rightarrow$ $V_C = r_cV_B=211.1\,\mathrm{cm}^3$

y la temperatura la ley de los gases ideales (o la ley de Charles, en este caso)

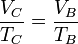
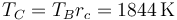
$\frac{V_C}{T_C}=\frac{V_B}{T_B}$ $\Rightarrow$ $T_C = T_B r_c = 1844\,\mathrm{K}$

5.4 Expansión adiabática

Durante la bajada del pistón el gas se enfría adiabáticamente. La temperatura al final del proceso la da la ley de Poisson, combinada con el que sabemos que el volumen al final es el mismo que antes de empezar la compresión

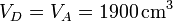
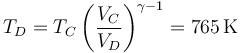
$V_D = V_A = 1900\,\mathrm{cm}^3$ $T_D = T_C\left(\frac{V_C}{V_D}\right)^{\gamma-1} = 765\,\mathrm{K}$

La presión en este estado es

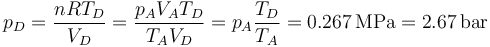
$p_D = \frac{nRT_D}{V_D}=\frac{p_AV_AT_D}{T_AV_D}=p_A\frac{T_D}{T_A}=0.267\,\mathrm{MPa}=2.67\,\mathrm{bar}$

5.5 Enfriamiento a V constante

En un motor diésel real el aire quemado y caliente es expulsado por el tubo de escape, liberando calor al ambiente y siendo sustituido por nuevo aire frío. En el ciclo Diesel ideal nos imaginamos que el aire recircula, volviendo al estado A, intercambiando sólo el calor con el ambiente.

Podemos hacer una tabla con los resultados

Estado	p (bar)	V (cm³)	T (K)
A	1.013	1900	190
B	57.9	105.6	922
C	57.9	211.1	1844
D	2.67	1900	765

5.6 Balance energético

5.6.1 Calor absorbido

El calor procedente del foco caliente es absorbido en la expansión a presión constante y es igual a

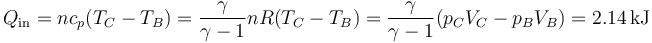
$Q_\mathrm{in} = nc_p(T_C-T_B) = \frac{\gamma}{\gamma-1}nR(T_C-T_B) = \frac{\gamma}{\gamma-1}(p_CV_C-p_BV_B)=2.14\,\mathrm{kJ}$

donde hemos usado que

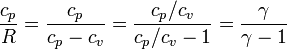
$\frac{c_p}{R}=\frac{c_p}{c_p-c_v}=\frac{c_p/c_v}{c_p/c_v-1}=\frac{\gamma}{\gamma-1}$

que para $γ = 1.4$ da el resultado conocido $c p = 3.5 R$ .

Un resultado más exacto para un proceso a presión constante, sin hacer uso de la hipótesis de gas ideal, consistiría en igualar el calor a la variación en la entalpía

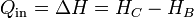
$Q_\mathrm{in} = \Delta H = H_C-H_B\,$

y aplicar valores tabulados de la entalpía del aire para las presiones y temperaturas de los estados B y C.

5.6.2 Calor cedido

El calor que se intercambia con el foco frío se cede en el enfriamiento a volumen constante

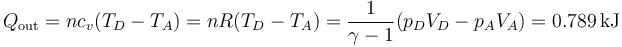
$Q_\mathrm{out} = nc_v(T_D-T_A) = nR(T_D-T_A) = \frac{1}{\gamma-1}(p_DV_D-p_AV_A)=0.789\,\mathrm{kJ}$

donde, como antes, hemos empleado la relación

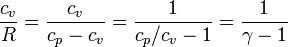
$\frac{c_v}{R}=\frac{c_v}{c_p-c_v}=\frac{1}{c_p/c_v-1}=\frac{1}{\gamma-1}$

que para $γ = 1.4$ da $c v = 2.5 R$ .

Si se quisiera hacer exactamente, habría que aplicar que para un proceso a volumen constante el calor equivale a la variación en la energía interna

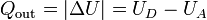
$Q_\mathrm{out} = |\Delta U| = U_D-U_A\,$

5.6.3 Trabajo realizado

El trabajo realizado por el sistema durante un ciclo es la diferencia entre el calor absorbido y el cedido (en valores absolutos)

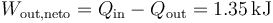
$W_\mathrm{out,neto} = Q_\mathrm{in}-Q_\mathrm{out} = 1.35\,\mathrm{kJ}$

5.6.4 Rendimiento

El rendimiento de este ciclo Diesel lo podemos hallar como el trabajo realizado dividido por el calor absorbido

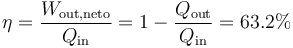
$\eta = \frac{W_\mathrm{out,neto}}{Q_\mathrm{in}} = 1-\frac{Q_\mathrm{out}}{Q_\mathrm{in}} = 63.2\%$

Vemos que el rendimiento es mucho mayor que para un ciclo Otto que, para valores típicos de motores de explosión, rondaba el 50%. La causa principal de la diferencia es la mucho mayor relación de compresión en el motor diésel.

5.6.5 Rendimiento de la segunda ley

El rendimiento de este ciclo Diesel es, por supuesto, inferior al de un ciclo de Carnot que operara entre las temperaturas $T A$ y $T C$ :

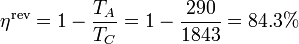
$\eta^\mathrm{rev}=1-\frac{T_A}{T_C} = 1-\frac{290}{1843}=84.3\%$

El rendimiento de la segunda ley nos lo da el cociente del rendimiento real respecto a este máximo.En comparación con este, el rendimiento del ciclo Diesel es

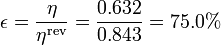
$\epsilon = \frac{\eta}{\eta^\mathrm{rev}}=\frac{0.632}{0.843} = 75.0\%$

es decir, tiene aproximadamente 3/4 del rendimiento máximo que podría tener.

5.6.6 Trabajo perdido

El trabajo perdido de una máquina térmica es la diferencia entre el máximo que podría conseguirse, para la entrada de calor dada y el que se consigue realmente

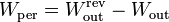
$W_\mathrm{per}=W^\mathrm{rev}_\mathrm{out}-W_\mathrm{out}\,$

En función del calor que entra y los rendimientos

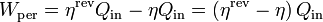
$W_\mathrm{per}= \eta^\mathrm{rev} Q_\mathrm{in}-\eta Q_\mathrm{in} = \left(\eta^\mathrm{rev}-\eta\right)Q_\mathrm{in}$

lo que nos da en nuestro caso

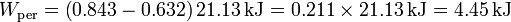
$W_\mathrm{per}= \left(0.843-0.632\right)21.13\,\mathrm{kJ} = 0.211\times 21.13\,\mathrm{kJ} =4.45\,\mathrm{kJ}$

Esto nos dice que 1/5 del calor que entra se desperdicia de más en forma de calor de desecho.

5.6.7 Producción de entropía

El trabajo perdido está directamente relacionado con la producción de entropía

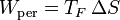
$W_\mathrm{per}=T_F\,\Delta S$

por lo que la producción de entropía para este caso particular vale

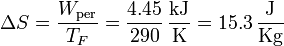
$\Delta S=\frac{W_\mathrm{per}}{T_F}=\frac{4.45}{290}\,\frac{\mathrm{kJ}}{\mathrm{K}}= 15.3\,\frac{\mathrm{J}}{\mathrm{Kg}}$

6 Comparación con el ciclo Otto

Según indicamos en la introducción, el ciclo Diesel ideal se distingue del Otto ideal en la fase de combustión, que en el ciclo Otto se supone a volumen constante y en el Diesel a presión constante. Por ello el rendimiento es diferente.

Si escribimos el rendimiento de un ciclo Diesel en la forma

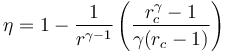
$\eta = 1 - \frac{1}{r^{\gamma-1}}\left(\frac{r_c^\gamma-1}{\gamma (r_c-1)}\right)$

vemos que la eficiencia de un ciclo Diesel se diferencia de la de un ciclo Otto por el factor entre paréntesis. Este factor siempre es mayor que la unidad, por ello, para iguales razones de compresión $r$

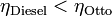
$\eta_\mathrm{Diesel}<\eta_\mathrm{Otto}\,$

Si la eficiencia del ciclo Diesel es menor que la del Otto, podría plantearse cuál es su interés. La ventaja que tiene es la mencionada de que, dado que solo comprime aire, su relación de compresión puede ser muy superior a la de un motor de gasolina, con lo que puede superar un rendimiento del ciclo Otto.

Por ejemplo, supongamos una relación de compresión $r = 8$ para ambos ciclos y una relación de combustión $r c = 2$ para el Diesel. En este caso, los rendimientos respectivos valen

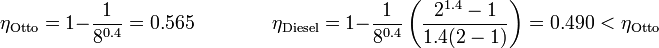
$\eta_\mathrm{Otto}=1-\frac{1}{8^{0.4}}=0.565\qquad\qquad \eta_\mathrm{Diesel}=1-\frac{1}{8^{0.4}}\left(\frac{2^{1.4}-1}{1.4(2-1)}\right)=0.490 < \eta_\mathrm{Otto}$

pero si aumentamos la relación de compresión para el ciclo Diesel a 12 obtenemos el rendimiento

$\eta_\mathrm{Otto}=1-\frac{1}{8^{0.4}}=0.565\qquad\qquad \eta_\mathrm{Diesel}=1-\frac{1}{12^{0.4}}\left(\frac{2^{1.4}-1}{1.4(2-1)}\right)=0.567 > \eta_\mathrm{Otto}$