No Boletín - Detección de invariantes (Ex.Feb/14)
De Laplace
1 Enunciado
En el contexto de la cinemática del sólido rígido, se utiliza la palabra "invariante" en un sentido espacial (no temporal). Por eso, se denomina invariante a cualquier magnitud cuyo valor no varía de un punto a otro del sólido rígido.
¿Cuál de las siguientes magnitudes no es un invariante?
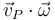 2)
2) 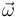 3)
3) 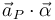 4)
4) 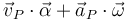
2 Solución
Averiguaremos si una magnitud es o no un invariante buscando la relación entre los valores que toma dicha magnitud en dos puntos arbitrarios ( y
y  ) del sólido rígido, para así poder comprobar si dichos valores son o no iguales entre sí.
) del sólido rígido, para así poder comprobar si dichos valores son o no iguales entre sí.
Utilizando la ecuación del campo de velocidades del sólido rígido:
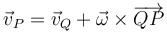
se comprueba que la primera magnitud propuesta (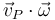 ) es un invariante:
) es un invariante:
![\vec{v}_{P}\cdot\vec{\omega}=\left[\vec{v}_{Q}+\vec{\omega}\times\overrightarrow{QP}\right]\cdot\vec{\omega}=\vec{v}_{Q}\cdot\vec{\omega}+\underbrace{\left[\vec{\omega}\times\overrightarrow{QP}\right]\!\cdot\vec{\omega}}_{=0\,\,\mathrm{(ortogonalidad)}}=\vec{v}_{Q}\cdot\vec{\omega}](/wiki/images/math/2/f/2/2f2c98d88af269a7ecb2fa17b089a1bc.png)
La segunda magnitud propuesta (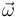 ) es también un invariante. No hace falta demostrarlo porque es obvio que su valor no varía de un punto a otro del sólido rígido, y además se trata del primer invariante fundamental estudiado en la teoría del tema.
) es también un invariante. No hace falta demostrarlo porque es obvio que su valor no varía de un punto a otro del sólido rígido, y además se trata del primer invariante fundamental estudiado en la teoría del tema.
Utilizamos ahora la ecuación del campo de aceleraciones del sólido rígido:
![\vec{a}_{P}=\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\vec{\omega}\times\left[\,\vec{\omega}\times\overrightarrow{QP}\,\right]=\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\left(\omega\cdot\overrightarrow{QP}\right)\vec{\omega}-\left|\vec{\omega}\right|^2\overrightarrow{QP}](/wiki/images/math/d/a/f/daffa0e57c342f4fe82bf1d69fb7e26b.png)
para analizar si la tercera magnitud propuesta (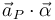 ) varía o no de valor al pasar de un punto a otro del sólido rígido:
) varía o no de valor al pasar de un punto a otro del sólido rígido:
![\vec{a}_{P}\,\cdot\,\vec{\alpha}=\left[\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\left(\omega\cdot\overrightarrow{QP}\right)\vec{\omega}-\left|\vec{\omega}\right|^2\overrightarrow{QP}\right]\cdot\,\vec{\alpha}=\vec{a}_{Q}\,\cdot\,\vec{\alpha}+\underbrace{\left(\vec{\alpha}\times\overrightarrow{QP}\right)\!\cdot\vec{\alpha}}_{=0\,\,\mathrm{(ortogonalidad)}}+\left(\omega\cdot\overrightarrow{QP}\right)\left(\vec{\omega}\cdot\vec{\alpha}\right)\,-\,\left|\vec{\omega}\right|^2\left(\overrightarrow{QP}\cdot\vec{\alpha}\right)](/wiki/images/math/8/6/3/86359c846a854f20276376c61d9606ff.png)
Observamos que los dos últimos sumandos no son nulos en general, de modo que:
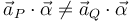
Por tanto, la tercera magnitud propuesta (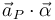 ) no es un invariante. Es la opción correcta conforme a la pregunta planteada en el enunciado.
) no es un invariante. Es la opción correcta conforme a la pregunta planteada en el enunciado.
Finalmente, nos queda comprobar que la cuarta magnitud propuesta (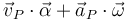 ) es también un invariante. Vamos a utilizar primero la ecuación del campo de velocidades de un sólido rígido para investigar el comportamiento ante el cambio de punto del primero de los dos sumandos que constituyen dicha magnitud:
) es también un invariante. Vamos a utilizar primero la ecuación del campo de velocidades de un sólido rígido para investigar el comportamiento ante el cambio de punto del primero de los dos sumandos que constituyen dicha magnitud:
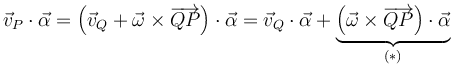
y a continuación utilizamos la ecuación del campo de aceleraciones de un sólido rígido para hacer lo propio con el segundo sumando:
![\vec{a}_{P}\,\cdot\,\vec{\omega}=\left[\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\vec{\omega}\times\left(\,\vec{\omega}\times\overrightarrow{QP}\,\right)\right]\cdot\,\vec{\omega}=\vec{a}_{Q}\,\cdot\,\vec{\omega}\,+\underbrace{\left(\vec{\alpha}\times\overrightarrow{QP}\right)\!\cdot\vec{\omega}}_{(**)}+\underbrace{\left[\vec{\omega}\times\left(\,\vec{\omega}\times\overrightarrow{QP}\,\right)\right]\!\cdot\vec{\omega}}_{=0\,\,\mathrm{(ortogonalidad)}}](/wiki/images/math/2/7/9/27918616386d0a587d643463a5855622.png)





