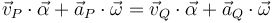No Boletín - Detección de invariantes (Ex.Feb/14)
De Laplace
Contenido |
1 Enunciado
En el contexto de la cinemática del sólido rígido, se utiliza la palabra "invariante" en un sentido espacial (no temporal). Por eso, se denomina invariante a cualquier magnitud cuyo valor no varía de un punto a otro del sólido rígido.
¿Cuál de las siguientes magnitudes no es un invariante?
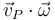 2)
2) 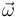 3)
3) 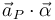 4)
4) 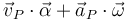
2 Primera magnitud propuesta
Averiguaremos si una magnitud es o no un invariante buscando la relación entre los valores que toma dicha magnitud en dos puntos arbitrarios ( y
y  ) del sólido rígido, para así poder comprobar si dichos valores son o no iguales entre sí.
) del sólido rígido, para así poder comprobar si dichos valores son o no iguales entre sí.
Utilizando la ecuación del campo de velocidades del sólido rígido:
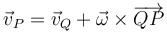
se comprueba que la primera magnitud propuesta (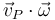 ) es un invariante:
) es un invariante:
![\vec{v}_{P}\cdot\vec{\omega}=\left[\vec{v}_{Q}+\vec{\omega}\times\overrightarrow{QP}\right]\cdot\vec{\omega}=\vec{v}_{Q}\cdot\vec{\omega}+\underbrace{\left[\vec{\omega}\times\overrightarrow{QP}\right]\!\cdot\vec{\omega}}_{=\,0\,\,\mathrm{(ortogonalidad)}}=\vec{v}_{Q}\cdot\vec{\omega}](/wiki/images/math/a/2/b/a2be90b04a790e4f2745b7e0324d1770.png)
3 Segunda magnitud propuesta
La segunda magnitud propuesta (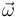 ) es también un invariante. No hace falta demostrarlo porque es obvio que su valor no varía de un punto a otro del sólido rígido, y además se trata del primer invariante fundamental estudiado en la teoría del tema.
) es también un invariante. No hace falta demostrarlo porque es obvio que su valor no varía de un punto a otro del sólido rígido, y además se trata del primer invariante fundamental estudiado en la teoría del tema.
4 Tercera magnitud propuesta
Utilizamos ahora la ecuación del campo de aceleraciones del sólido rígido:
![\vec{a}_{P}=\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\,\vec{\omega}\times\left[\,\vec{\omega}\times\overrightarrow{QP}\,\right]=\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\left(\omega\cdot\overrightarrow{QP}\right)\vec{\omega}-\left|\vec{\omega}\right|^2\overrightarrow{QP}](/wiki/images/math/7/e/4/7e45fe8271c4fbba7bb1977e966b17c7.png)
para analizar si la tercera magnitud propuesta (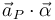 ) varía o no de valor al pasar de un punto a otro del sólido rígido:
) varía o no de valor al pasar de un punto a otro del sólido rígido:
![\vec{a}_{P}\,\cdot\,\vec{\alpha}=\left[\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\left(\omega\cdot\overrightarrow{QP}\right)\vec{\omega}-\left|\vec{\omega}\right|^2\overrightarrow{QP}\right]\cdot\,\vec{\alpha}=\vec{a}_{Q}\,\cdot\,\vec{\alpha}\,+\underbrace{\left(\vec{\alpha}\times\overrightarrow{QP}\right)\!\cdot\vec{\alpha}}_{=\,0\,\,\mathrm{(ortogonalidad)}}+\underbrace{\left(\omega\cdot\overrightarrow{QP}\right)\left(\vec{\omega}\cdot\vec{\alpha}\right)\,-\,\left|\vec{\omega}\right|^2\left(\overrightarrow{QP}\cdot\vec{\alpha}\right)}_{\neq\, 0\,\,\mathrm{(en}\,\,\mathrm{general)}}](/wiki/images/math/c/6/c/c6cfd153f00d49c3783e6fa3948d82be.png)
Observamos que los dos últimos sumandos son no nulos en general, de modo que:
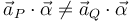
Por tanto, la tercera magnitud propuesta (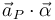 ) no es un invariante. Ésta es la opción correcta conforme a la pregunta planteada en el enunciado.
) no es un invariante. Ésta es la opción correcta conforme a la pregunta planteada en el enunciado.
5 Cuarta magnitud propuesta
Finalmente, nos queda comprobar que la cuarta magnitud propuesta (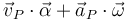 ) es un invariante. Utilizamos la ecuación del campo de velocidades del sólido rígido para investigar el comportamiento ante un cambio de punto del primero de los dos sumandos que constituyen dicha magnitud:
) es un invariante. Utilizamos la ecuación del campo de velocidades del sólido rígido para investigar el comportamiento ante un cambio de punto del primero de los dos sumandos que constituyen dicha magnitud:
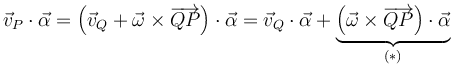
y utilizamos la ecuación del campo de aceleraciones del sólido rígido para hacer lo propio con el segundo sumando de la magnitud:
![\vec{a}_{P}\,\cdot\,\vec{\omega}=\left[\vec{a}_{Q}+\vec{\alpha}\times\overrightarrow{QP}+\vec{\omega}\times\!\left(\,\vec{\omega}\times\overrightarrow{QP}\,\right)\right]\cdot\,\vec{\omega}=\vec{a}_{Q}\,\cdot\,\vec{\omega}\,\,+\,\underbrace{\left(\vec{\alpha}\times\overrightarrow{QP}\right)\!\cdot\vec{\omega}}_{(**)}\,+\underbrace{\left[\,\vec{\omega}\times\!\left(\,\vec{\omega}\times\overrightarrow{QP}\,\right)\right]\!\cdot\vec{\omega}}_{=\,0\,\,\mathrm{(ortogonalidad)}}](/wiki/images/math/3/1/d/31d93d92d1eff86842f3cfe0b48b2b1b.png)
Obsérvese que los términos que hemos marcado como (*) y (**) son opuestos entre sí, ya que una permutación no cíclica en un producto mixto equivale a un cambio de signo. Por tanto, al sumar para recuperar la cuarta magnitud propuesta, los términos (*) y (**) se cancelan mutuamente permitiéndonos concluir que en efecto 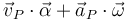 es un invariante:
es un invariante: