Masa que cuelga de una cámara de aire

De Laplace

Revisión a fecha de 16:38 20 mar 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Descenso del pistón
4 Calor
5 Ascenso gradual del pistón
6 Variación de entropía
7 Caso adiabático

1 Enunciado

Se tiene una balanza formada por un recipiente cilíndrico de 16 cm² de sección lleno de aire (considerado como un gas ideal). El tubo está cerrado herméticamente en su parte inferior por un émbolo que puede deslizarse sin rozamiento y que tiene un gancho en su cara inferior. Las paredes y el émbolo no están aislados térmicamente. Inicialmente el émbolo se encuentra a 15 cm de la pared superior, y el gas en equilibrio mecánico y térmico con el exterior, que se halla a 1 bar y 300 K. Se cuelga bruscamente del pistón un saco de harina de 4 kg.

¿Cuánto desciende aproximadamente el pistón hasta que se alcanza de nuevo el equilibrio?
¿Cuánto vale aproximadamente el calor que entra en el sistema en este proceso?
Suponga que el saco tiene un agujero, de forma que la harina se escapa lentamente hasta vaciarse por completo (despreciamos el peso del propio saco). ¿Cuánto vale el calor que entra en el sistema en este segundo proceso?
¿Cuánto varía la entropía del sistema, del ambiente del universo en el descenso? ¿Y en el ascenso ulterior?
Supongamos que la cámara y el pistón están aislados térmicamente, de manera que los procesos son adiabáticos. ¿Cómo quedan en ese caso los resultados de los apartados anteriores?

2 Introducción

Este problema es casi idéntico al “Trabajo en una compresión por un peso”, siendo la única diferencia esencial el que en ese otro problema la masa comprime el gas, aumentando la presión y en este lo expande, reduciéndola. No obstante, lo resolveremos de forma completa también aquí.

3 Descenso del pistón

Inicialmente (estado A) tenemos un gas a una presión y temperatura

$p_A=p_0=10^5\,\mathrm{Pa}\qquad\qquad T_A=300\,\mathrm{K}$

y que ocupa un volumen

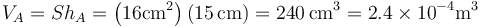
$V_A=Sh_A=\left(16\mathrm{cm}^2\right)(15\,\mathrm{cm})=240\,\mathrm{cm}^3= 2.4\times 10^{-4}\mathrm{m}^3$

Cuando se cuelga el peso del pistón, disminuye la fuerza aplicada exteriormente sobre el gas, ya que a la presión atmosférica, que empuja hacia arriba hay que restarle la contribución del peso, que va hacia abajo. En ese momento la presión interior supera a la fuerza exterior y el gas se expande reduciendo su presión, hasta un nuevo valor $p B$ .

El equilibrio se alcanza cuando la suma de fuerzas vuelve a ser nula. Considerando positivas las fuerzas que van hacia arriba y negativas las que van hacia abajo, sería

$-p_BS+p_0S-mg = 0\,$

de donde la nueva presión interior vale

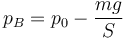
$p_B = p_0-\frac{mg}{S}$

El resultado es idéntico al del otro problema, sin más que cambiar el signo del peso.

Podría pensarse que la nueva presión podría llegar a ser negativa, pero no es así. La presión atmosférica es tan grande que lo que se reduce por la acción del peso es solo una parte relativamente pequeña. Concretamente, tomando g = 10m/s²,

$p_0=100\,000\,\mathrm{Pa}\qquad\qquad \frac{mg}{S}= 25\,000\,\mathrm{Pa}$

es decir, los 4kg ejercen una fuerza que es solo una cuarta parte de la que realiza la atmósfera. Lo que estamos describiendo es el mismo principio que hace funcionar las ventosas. Podemos colgar una masa pequeña de una de ellas porque la presión atmosférica la mantiene sujeta debido a la diferencia de presiones. Eso sí, si se hiciera un orificio penetraría el aire exterior, se igualarían las presiones y el peso caería llevándose el pistón o la ventosa.

La nueva presión de equilibrio es entonces

$p_B = p_0 - \frac{mg}{S}=75000\,\mathrm{Pa}$

Puesto que la temperatura no ha cambiado, podemos hallar el nuevo volumen empleando la ley de Boyle

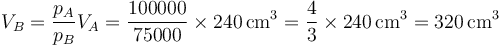
$V_B = \frac{p_A}{p_B}V_A=\frac{100000}{75000}\times 240\,\mathrm{cm}^3=\frac{4}{3}\times 240\,\mathrm{cm}^3=320\,\mathrm{cm}^3$

siendo la nueva distancia del pistón al techo

$h_B = \frac{V_B}{S}=\frac{p_A}{p_B}h_A=\frac{4}{3}15\,\mathrm{cm}=20\,\mathrm{cm}$

y el desplazamiento

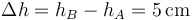
$\Delta h = h_B-h_A=5\,\mathrm{cm}$

4 Calor

En este proceso la temperatura del gas es la misma al principio y al final del proceso, por lo que su energía interna no cambia

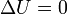
$\Delta U = 0\,$

Por el primer principio de la termodinámica esto implica que se anula la suma del calor y el trabajo que entran en el gas en el proceso

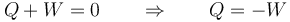
$Q+W=0\qquad\Rightarrow\qquad Q=-W$

El trabajo que entra en el sistema es debido a la presión externa ejercida sobre él

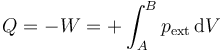
$Q=-W=+\int_A^Bp_\mathrm{ext}\,\mathrm{d}V$

En esta expansión la presión ejercida desde el exterior es constante y equivale a la atmosférica menos la contribución debida al peso

$p_\mathrm{ext}=p_B=p_0-\frac{mg}{S}$

lo que nos da el calor

$Q=p_B(V_B-V_A)\,$

Aquí podemos sustituir ya los valores numéricos

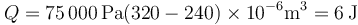
$Q=75\,000\,\mathrm{Pa}(320-240)\times 10^{-6}\mathrm{m}^3=6\,\mathrm{J}$

Algebráicamente podemos hallar una expresión más simple con ayuda de la ley de Boyle

$Q=p_BV_B-p_BV_A=p_AV_A-p_BV_A=(p_A-p_B)V_A\,$

que en términos del peso queda

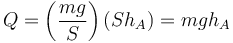
$Q=\left(\frac{mg}{S}\right)(Sh_A)=mgh_A$

Numéricamente

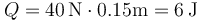
$Q = 40\,\mathrm{N}\cdot 0.15\mathrm{m}=6\,\mathrm{J}$

Este calor es positivo ya que al expandirse el gas realiza trabajo sobre el ambiente. Puesto que su energía interna no disminuye, esta salida de trabajo debe ser compensada por una entrada de calor

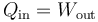
$Q_\mathrm{in}=W_\mathrm{out}\,$

5 Ascenso gradual del pistón

Una vez que se ha alcanzado el equilibrio, la masa de harina se va reduciendo progresivamente a medida que va cayendo harina del saco. Esto equivale a que la presión exterior va aumentando (ya que cada vez le restamos menos a la atmosférica), y el aire se vuelve a comprimir. En el nuevo estado final (estado C), la presión vuelve a ser la inicial. Puesto que la temperatura también es igual a la inicial, este estado C es igual al inicial, A.

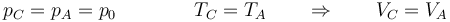
$p_C=p_A=p_0\qquad\qquad T_C=T_A\qquad\Rightarrow\qquad V_C = V_A$

Al caer la harina lentamente, este segundo proceso puede suponerse cuasiestático. En este caso, en cada momento la presión interior equivale a la exterior, por lo que

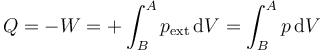
$Q = -W = +\int_B^A p_\mathrm{ext}\,\mathrm{d}V=\int_B^A p\,\mathrm{d}V$

Puesto que la temperatura permanece constante, se trata de un proceso isotermo y cuasiestático. Aplicando la ley de Boyle

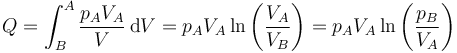
$Q=\int_B^A \frac{p_AV_A}{V}\,\mathrm{d}V=p_AV_A\ln\left(\frac{V_A}{V_B}\right)=p_AV_A\ln\left(\frac{p_B}{V_A}\right)$

resultando el valor numérico para el calor

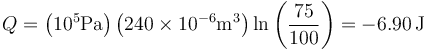
$Q=\left(10^5\mathrm{Pa}\right)\left(240\times 10^{-6}\mathrm{m}^3\right)\ln\left(\frac{75}{100}\right) = -6.90\,\mathrm{J}$

Vemos que el calor que sale en la compresión cuasiestático no coincide en magnitud con el que entra en la compresión no cuasiestático

6 Variación de entropía

7 Caso adiabático

Masa que cuelga de una cámara de aire

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Descenso del pistón

4 Calor

5 Ascenso gradual del pistón

6 Variación de entropía

7 Caso adiabático

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES