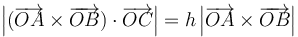Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Arista de un tetraedro (Ex.Oct/13)

De Laplace

1 Enunciado

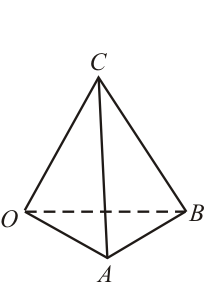
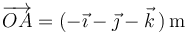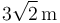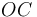El triángulo definido por los vectores \overrightarrow{OA}=(-\vec{\imath}-\vec{\jmath}-\vec{k}\,)\, \mathrm{m}\, y \overrightarrow{OB}=2\,\vec{k}\,\,\mathrm{m}\, constituye la base de un tetraedro. Sabiendo que la altura de dicho tetraedro es 3\sqrt{2}\,\mathrm{m}\, y que C\, es el vértice opuesto a su base, ¿cuál de los siguientes vectores puede definir la arista OC\, del tetraedro descrito?

1) \overrightarrow{OC}=(\vec{\imath}+\vec{\jmath}-\vec{k}\,)\,\mathrm{m}\,

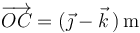
2) \overrightarrow{OC}=(\vec{\jmath}-\vec{k}\,)\,\mathrm{m}\,

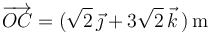
3) \overrightarrow{OC}=(\sqrt{2}\,\vec{\jmath}+3\sqrt{2}\,\vec{k}\,)\,\mathrm{m}\,

4) \overrightarrow{OC}=(-2\,\vec{\imath}+4\,\vec{\jmath}+\vec{k}\,)\,\mathrm{m}\,

2 Solución

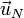Se calcula un vector \vec{N}\, normal a la base del tetraedro, y dividiéndolo por su módulo (normalización) se obtiene un vector unitario \vec{u}_N\, en su misma dirección:

\vec{N}=\overrightarrow{OA}\,\times\,\overrightarrow{OB}=\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -1 & -1 & -1 \\ 0 & 0 & 2 \end{array}\right|=-2\,\vec{\imath}\,+\,2\,\vec{\jmath}\,\,\,\,\,\longrightarrow\,\,\,\,\, \vec{u}_N=\frac{\vec{N}}{|\vec{N}|}=\frac{-2\,\vec{\imath}+2\,\vec{\jmath}}{2\sqrt{2}}=-\frac{1}{\sqrt{2}}\,\vec{\imath}\,\,+\,\frac{1}{\sqrt{2}}\,\vec{\jmath}\,

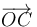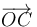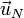A continuación, se observa por inspección geométrica que la altura del tetraedro coincide con el valor absoluto de la proyección del vector-arista \overrightarrow{OC}\, sobre la dirección normal a la base. Así que dicha altura h\, se puede calcular como el valor absoluto del producto escalar del vector \overrightarrow{OC}\, por el vector unitario \vec{u}_N\,:

h=\left|\mathrm{proy}_{\parallel\vec{N}}\left[\overrightarrow{OC}\right]\right|=\left|\overrightarrow{OC}\cdot\vec{u}_N\right|=\left|-\frac{OC_x}{\sqrt{2}}\,+\,\frac{OC_y}{\sqrt{2}}\right|

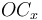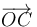donde hemos denominado OC_x\, y OC_y\, a la componente-x y a la componente-y, respectivamente, del vector \overrightarrow{OC}\,.

Como la altura del tetraedro es conocida (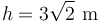h=3\sqrt{2}\,\,\mathrm{m}\,), sólo queda comprobar cuál de los cuatro vectores 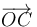\overrightarrow{OC}\, propuestos en el enunciado satisface la siguiente condición:

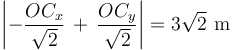
\left|-\frac{OC_x}{\sqrt{2}}\,+\,\frac{OC_y}{\sqrt{2}}\right|=3\sqrt{2}\,\,\mathrm{m}

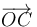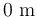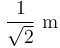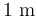Es inmediato verificar que el vector \overrightarrow{OC}\, propuesto en la opción 4 es el correcto (los de las opciones 1, 2 y 3 implican una altura del tetraedro igual a 0\,\,\mathrm{m}\,, \displaystyle\frac{1}{\sqrt{2}}\,\,\mathrm{m}\, y 1\,\,\mathrm{m}\,, respectivamente).

3 Solución alternativa

Podemos simplificar un poco el cálculo sin usar tantas raíces cuadradas observando que puesto que

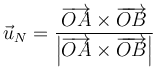
\vec{u}_N=\frac{\overrightarrow{OA}\times\overrightarrow{OB}}{\left|\overrightarrow{OA}\times\overrightarrow{OB}\right|}

la ecuación que define la altura es

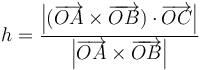
h = \frac{\left|(\overrightarrow{OA}\times\overrightarrow{OB})\cdot\overrightarrow{OC}\right|}{\left|\overrightarrow{OA}\times\overrightarrow{OB}\right|}

o, equivalentemente

\left|(\overrightarrow{OA}\times\overrightarrow{OB})\cdot\overrightarrow{OC}\right| = h \left|\overrightarrow{OA}\times\overrightarrow{OB}\right|
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Arista_de_un_tetraedro_(Ex.Oct/13)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace