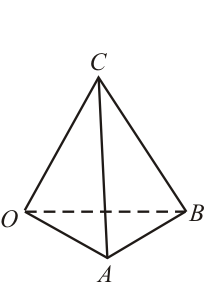
Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Arista de un tetraedro (Ex.Oct/13)

De Laplace

1 Enunciado

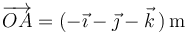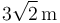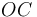El triángulo definido por los vectores \overrightarrow{OA}=(-\vec{\imath}-\vec{\jmath}-\vec{k}\,)\, \mathrm{m}\, y \overrightarrow{OB}=2\,\vec{k}\,\,\mathrm{m}\, constituye la base de un tetraedro. Sabiendo que la altura de dicho tetraedro es 3\sqrt{2}\,\mathrm{m}\, y que C\, es el vértice opuesto a su base, ¿cuál de los siguientes vectores puede definir la arista OC\, del tetraedro descrito?

1) \overrightarrow{OC}=(\vec{\imath}+\vec{\jmath}-\vec{k}\,)\,\mathrm{m}\,

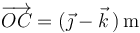
2) \overrightarrow{OC}=(\vec{\jmath}-\vec{k}\,)\,\mathrm{m}\,

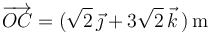
3) \overrightarrow{OC}=(\sqrt{2}\,\vec{\jmath}+3\sqrt{2}\,\vec{k}\,)\,\mathrm{m}\,

4) \overrightarrow{OC}=(-2\,\vec{\imath}+4\,\vec{\jmath}+\vec{k}\,)\,\mathrm{m}\,

2 Solución

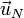Se calcula un vector \vec{N}\, normal a la base del tetraedro, y dividiéndolo por su módulo (normalización) se obtiene un vector unitario \vec{u}_N\, en su misma dirección:

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{N}=\overrightarrow{OA}\times\overrightarrow{OB}=\left|\vec{\imath} & \vec{\jmath} & \vec{k} // -1 & -1 & -1 // 0 & 0 & 2 \end{array}\right|=-2\,\vec{\imath}+2\,\vec{\jmath}\,\,\,\,\,\longrightarrow\,\,\,\,\, \vec{u}_N=\frac{\vec{N}}{|\vec{N}|}=\frac{-2\,\vec{\imath}+2\,\vec{\jmath}}{2\sqrt{2}}=-\frac{1}{\sqrt{2}}\,\vec{\imath}+\frac{1}{\sqrt{2}}\,\vec{\jmath}\,

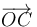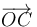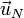A continuación, se observa por inspección geométrica que la altura del tetraedro coincide con el valor absoluto de la proyección del vector-arista \overrightarrow{OC}\, sobre la dirección normal a la base. Así que dicha altura h\, se puede calcular como el valor absoluto del producto escalar del vector \overrightarrow{OC}\, por el vector unitario \vec{u}_N\,:

h=\left|\mathrm{proy}_{\parallel\vec{N}}\left[\overrightarrow{OC}\right]\right|=\left|\overrightarrow{OC}\cdot\vec{u}_N\right|=\left|\overrightarrow{OC}\cdot\frac{\overrightarrow{OA}\times\overrightarrow{OB}}{|\overrightarrow{OA}\times\overrightarrow{OB}|}\right|=\frac{|\overrightarrow{OC}\cdot(\overrightarrow{OA}\times\overrightarrow{OB})|}{|\overrightarrow{OA}\times\overrightarrow{OB}|}=\frac{|\overrightarrow{OA}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})|}{|\overrightarrow{OA}\times\overrightarrow{OB}|}
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Arista_de_un_tetraedro_(Ex.Oct/13)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace