No Boletín - Arista de un tetraedro (Ex.Oct/13)
De Laplace
Revisión a fecha de 17:22 18 mar 2014; Enrique (Discusión | contribuciones)
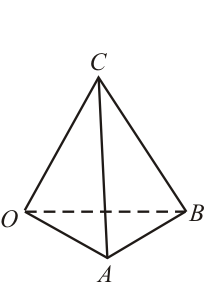
1 Enunciado
El triángulo definido por los vectores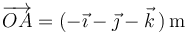 
y
constituye la base de un tetraedro. Sabiendo que la altura de dicho tetraedro es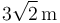 
y que 
es el vértice opuesto a su base, ¿cuál de los siguientes vectores puede
definir la arista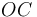 
del tetraedro descrito?
1) 
2) 
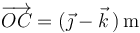
3) 
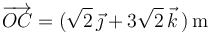
4) 
