Potencial en gota de agua cargada eléctricamente FII GIA
De Laplace
Contenido |
1 Enunciado
Una gota esférica de agua transporta una carga de 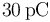 uniformemente distribuida en su volumen, siendo el potencial en su
superficie de
uniformemente distribuida en su volumen, siendo el potencial en su
superficie de 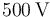 (considerando V = 0 en el infinito).
(considerando V = 0 en el infinito).
- ¿Cuál es el radio de la gota?
- ¿Cuál es el valor del potencial en el centro de la gota?
- Si esta gota se combina con otra con el mismo radio y la misma carga para formar una sola gota, determine el potencial en la superficie de la nueva gota.
2 Solución
Para resolver el ejercicio se propone como modelo que la carga eléctrica 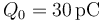 se distribuye uniformemente en todo el volumen de la gota, que consideraremos como una esfera
se distribuye uniformemente en todo el volumen de la gota, que consideraremos como una esfera 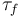 de centro O y radio R desconocido. Por tanto, aunque dicha distribución estará caracterizada por una densidad volumétrica de carga constante ρ0, desconocemos su valor a priori:
de centro O y radio R desconocido. Por tanto, aunque dicha distribución estará caracterizada por una densidad volumétrica de carga constante ρ0, desconocemos su valor a priori:
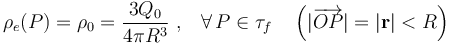
Como el dato conocido es que el potencial electrostático en la superficie de la gota tiene un valor de 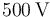 , hemos de utilizar la función
, hemos de utilizar la función 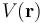 para dicho campo escalar. Recordemos cómo se obtiene dicha función de campo:
para dicho campo escalar. Recordemos cómo se obtiene dicha función de campo:
2.1 Potencial electrostático creado por una esfera cargada uniformemente
Como se sabe, conocido el valor de potencial en un determinado punto P0 del espacio, V(P0) = V0, para cualquier otro punto P se tendrá:
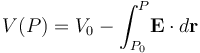
Considerando que la posición del punto genérico P está determinada por el radio-vector posición 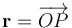 , la expresión general de la función de campo puede expresarse en términos de una integral indefinida para el campo eléctrico más una constante de integración, que ha de ajustarse de manera que se verifique la condición sobre el valor conocido del potencial para
, la expresión general de la función de campo puede expresarse en términos de una integral indefinida para el campo eléctrico más una constante de integración, que ha de ajustarse de manera que se verifique la condición sobre el valor conocido del potencial para 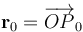 :
:
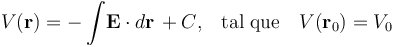
El campo eléctrico creado por distribución uniformemente de carga en la esfera, presentará expresiones distintas dentro y fuera de dicha distribución:
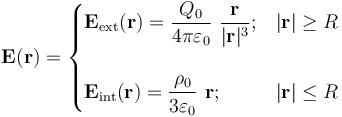
En consecuencia, el potencial también estará definido por expresiones diferentes en cada una de las dos regiones consideradas:
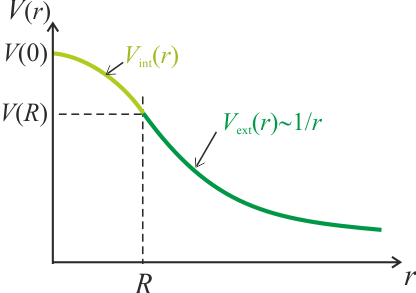
2.1.1 Potencial en el exterior
En los puntos exteriores a la distrución de carga se tendrá:
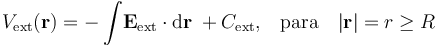
Si expresamos el vector-posición  en términos de su módulo r y del vector unitario
en términos de su módulo r y del vector unitario 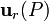 , en la dirección y el sentido del sentido del segmento
, en la dirección y el sentido del sentido del segmento  , se obtiene:
, se obtiene:

pues al ser 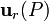 un vector de módulo constante (siempre igual a la unidad), en todo punto se cumplirá que
un vector de módulo constante (siempre igual a la unidad), en todo punto se cumplirá que 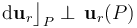 . En consecuencia, el potencial electrostático creado en el exterior de la distribución esférica de será:
. En consecuencia, el potencial electrostático creado en el exterior de la distribución esférica de será:
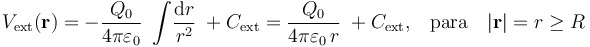
La constante de integración Cext se ha de determinar a partir de valor del potencial en un punto del dominio de definición; es decir, un punto del exterior. Obsérvese que los puntos infinitamente alejados de la distribución pertenecen a dicho dominio, y puesto que la carga Q0 se distribuye en una región finita (la esfera de radio R), la perturbación que produce (es decir, el campo eléctrico o el potencial electrostático) va a ser poco significativa e incluso despreciable en puntos muy alejados. En consecuencia, la constante de integración Cext debe ser tal que:
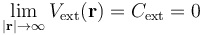

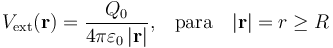
2.1.2 Potencial en el interior
En el interior de la distribución volumétrica uniforme de carga se tendrá: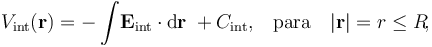
donde el integrando se obtiene utilizando la expresión del cargo eléctrico en dicha región,
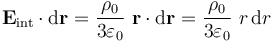
obteniéndose la expresión general:
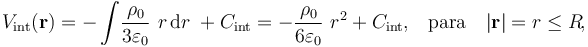
Para determinar el valor de la constante de integración Cint debemos, nuevamente, utilizar el valor del potencial en un punto del dominio de definición. Sin embargo, en esta ocasión no podemos adjudicar un valor arbitrario de potencial en un punto cualquiera, sino que hemos de aplicar la condición de continuidad del potencial en los puntos de la superficie o interfaz que separa las regiones exterior e interior. En este caso se tratataría de la superficie esférica Σ de la gota cargada, cuyo radio R desconocemos:
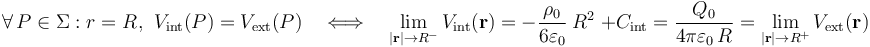
Teniendo en cuenta la relación entre la cantidad total de carga en la gota Q0, y la densidad volumétrica constante ρ0 con la que se distribuye, se obtiene qué valor ha de tener la constante de integraciónEs decir, para que el potencial sea continuo en la superficie de la gota:
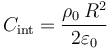

![V_\mathrm{int}(\mathbf{r})=\frac{\rho_0\!\ R^2}{2\varepsilon_0}\!\ \left[1-\frac{|\mathbf{r}|^2}{3\!\ R^2}\right]=\frac{3\!\ Q_0}{8\pi\varepsilon_0\!\ R}\!\ \left[1-\frac{|\mathbf{r}|^2}{3\!\ R^2}\right]\mathrm{,}\quad\mathrm{para}\quad|\mathbf{r}|=r\leq R](/wiki/images/math/3/8/4/3843477152dcacc101b6a6c3ecca0f60.png)
2.2 Radio de la gota
A patir de los resultados generales obtenidos en el apartado anterior, podemos determinar el radio de la gota en el sistema bajo estudio. En el enunciado se indica que le potencial electrostático en la superficie Σ de la gota tiene un valor conocido:
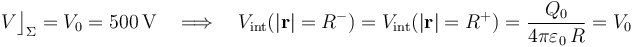
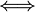
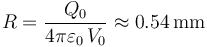
donde, además del valor de potencial V0, se han utilizado los valores de carga total en la gota y de la constante electrostática, 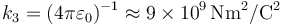
2.3 Valor del potencial en el centro de la gota
Los resultados del primer apartado también nos permiten determinar el valor en el centro O de la distribución de carga, una vez determinado el radio de la gota:
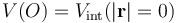

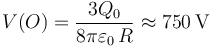
Obsérvese que, si se conoce el radio del gota y el potencial en cualquier punto 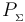 de su superficie, es posible determinar el potencial en el centro O teniendo en cuenta que la diferencia de potencial entre ambos puntos debe ser igual a la circulación del campo eléctrio entre ambos puntos. Este resultado debe ser independiente del camino elegido, por lo que si evaluamos dicha circulación en una trayectoria que tiene todos sus puntos en el interior de la gota, se tendrá:
de su superficie, es posible determinar el potencial en el centro O teniendo en cuenta que la diferencia de potencial entre ambos puntos debe ser igual a la circulación del campo eléctrio entre ambos puntos. Este resultado debe ser independiente del camino elegido, por lo que si evaluamos dicha circulación en una trayectoria que tiene todos sus puntos en el interior de la gota, se tendrá:
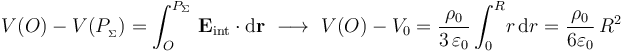



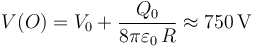
2.4 Gota doble
Consideramos ahora el caso en que dos gotas idénticas a las analizadas en los apartados anteriores, de igual radio 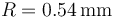 y volumen, y con la misma cantidad de carga
y volumen, y con la misma cantidad de carga 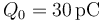 cada una de ellas, se une para formar una única gota. Ésta tendrá el doble de volumen que las anteriores y también el doble de carga, por lo que la densidad volumétrica de carga eléctrica no habrá cambiado:
cada una de ellas, se une para formar una única gota. Ésta tendrá el doble de volumen que las anteriores y también el doble de carga, por lo que la densidad volumétrica de carga eléctrica no habrá cambiado:
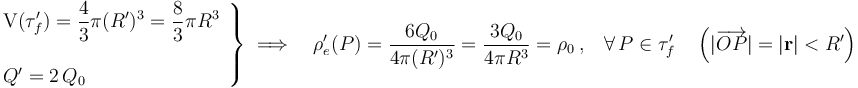
En consecuencia, el potencial electrostático creado por la carga de la nueva gota, será análogo al de los apartados anteriores, teniendo en cuenta que ahora la cantidad de carga es el doble y que el radio debe ser tal que el volumen también sea el doble:
![V (\mathbf{r})=\begin{cases}\displaystyle V_\mathrm{ext}(\mathbf{r})=\frac{Q_0}{4\pi\varepsilon_0\!\ |\mathbf{r}|}\ \mathrm{;}&|\mathbf{r}|\geq R^\prime\\ \\ \displaystyle V_\mathrm{int}(\mathbf{r})=\frac{6\!\ Q_0}{8\pi\varepsilon_0\!\ R^\prime}\!\ \left[1-\frac{|\mathbf{r}|^2}{3\!\ (R^\prime)^2}\right]\mathrm{;}&|\mathbf{r}|=r\leq R^\prime\end{cases}](/wiki/images/math/0/1/0/0107a097fbb309e768a9aca889436c2a.png)
siendo 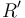 tal que
tal que