Test de la prueba de control 2013-2014 (GIE)
De Laplace
Contenido |
1 Velocidad cuadrática con la posición
Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto v = − kx2. Su posición inicial es x(t = 0) = x0
1.1 Pregunta 1
¿Cuáles son las unidades de k en el SI
- A 1/(m·s)
- B m\tss{3}/s
- C m/s
- D m/s²
1.1.1 Solución
La respuesta correcta es la A.
Por homogeneidad dimensional, debe ser
![[v]=[k][x]^2\qquad\Rightarrow\qquad \frac{L}{T}=[k]\frac{L^2}{T^2}\qquad\Rightarrow\qquad [k]=\frac{1}{L\cdot T}](/wiki/images/math/a/e/e/aee6c6a93ad7a9ba2e71989aa4e18d87.png)
con lo que su unidad en el SI será 1/m·s.
1.2 Pregunta 2
¿Cuánto vale la aceleración de la partícula cuando se halla en un punto x?
- A 0.
- B 2k²x³.
- C No hay información suficiente para calcularla.
- D −2kx.
1.2.1 Solución
La respuesta correcta es la B.
Derivamos respecto al tiempo aplicando la regla de la cadena
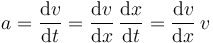
lo cual nos da
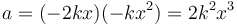
1.3 Pregunta 3
¿Cuánto vale la posición como función del tiempo?
- A
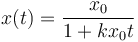
- B
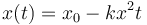
- C No hay información suficiente para calcularla.
- D
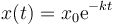
- A
1.3.1 Solución
La respuesta correcta es la A.
Podemos separar los diferenciales en la expresión de la derivada
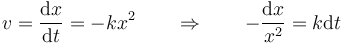
Integrando aquí desde la posición inicial
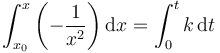
y queda
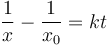
Despejando la posición
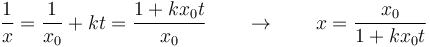
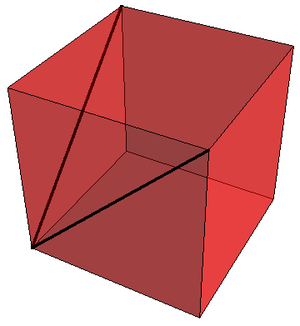
2 Ángulo entre diagonales
Se tienen dos vectores a lo largo de las diagonales de las caras de un cubo, con el mismo punto de aplicación. ¿Qué ángulo forman?
- A π / 4
- B π / 6
- C π / 2
- D π / 3
2.1 Solución
La respuesta correcta es la D.
3 Movimiento en polares
Una partícula se mueve de forma que en el SI sus coordenadas polares valen, en todo instante t > 0,
¿Cuánto vale su rapidez en 
?
- A 5 m/s
- B 4 m/s
- C 10 m/s
- D
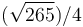m/s
3.1 Solución
La respuesta correcta es la A.
4 Condición de movimiento uniforme
¿Cuál de las siguientes condiciones no define un movimiento uniforme?
- A La distancia recorrida aumenta linealmente con el tiempo.
- B El vector tangente es constante.
- C La rapidez es constante.
- D La aceleración tangencial es nula.
4.1 Solución
La respuesta correcta es la B.
5 Movimiento en polares
Una partícula describe un movimiento armónico simple con frecuencia angular 2 rad/s, siendo el fasor de la elongación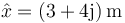 
. ¿Cuánto vale su velocidad inicial?
- A No hay información suficiente para determinarla.
- B 2 m/s
- C −8 m/s
- D −2 m/s
5.1 Solución
La respuesta correcta es la C.
6 Aceleración de la Tierra
Sabiendo que la distancia de la Tierra al Sol es de 150 millones de kilómetros, ¿cuánto vale aproximadamente la aceleración normal de la Tierra en su movimiento de traslación alrededor del Sol?
- A 30000 m/s²
- B 0.006 m/s²
- C 6.0 m/s²
- D 0.034 m/s²
6.1 Solución
La respuesta correcta es la B.
