Preguntas de test de dinámica del sólido rígido (GIE)
De Laplace
Contenido |
1 Momento de inercia de un péndulo
Se tiene un péndulo compuesto formado por una bola de masa 2 kg y diámetro 10 cm que oscila verticalmente colgada por un ganchito de un hilo de masa despreciable y que mide 20 cm, atado a la pared. ¿Cuánto vale el momento de inercia del péndulo respecto a un eje perpendicular al plano de oscilación y que pasa por el punto de anclaje del hilo en la pared?
- A 0.002 kg·m².
- B 0.050 kg·m².
- C 0.008 kg·m².
- D 0.127 kg·m².
1.1 Solución
2 Dos fuerzas sobre una barra
En los extremos una barra rígida de longitud h en reposo se aplican dos fuerzas del mismo módulo según la dirección longitudinal de la barra y con sentido opuesto. El resultado de esta aplicación es…
- A una traslación de la barra.
- B una rotación en torno al centro de la barra.
- C un movimiento helicoidal de la barra.
- D ninguno. La barra permanece en reposo.
2.1 Solución
La respuesta correcta es la D.
Al ser las dos fuerzas opuestas, la resultante es nula.
Al estar aplicadas las dos sobre la misma recta, el brazo del par mide 0, y por tanto, el momento resultante también es nula. Si la barra estaba en reposo, continúa en reposo.
3 Comparación de dos momentos de inercia
Se tienen dos esferas macizas de acero, tales que R2 = 2R1. ¿Cuál es la proporción entre los momentos de inercia de ambas respecto a un eje que pasa por sus centros, I2 / I1?
- A 2.
- B 32.
- C 4.
- D 8.
3.1 Solución
La respuesta correcta es la B.
El cociente entre los dos momentos de inercia es igual a
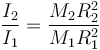
(el factor 2/5 de cada momento de inercia se cancela). Al ser R2 = 2R1 se cumple que
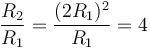
pero también que
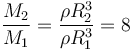
(sabemos que la densidad es la misma pues se nos dicen que las dos bolas son de acero). Por tanto
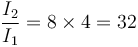
4 Sólido formado por tres partículas
Un sólido está formado por tres partículas, una de masa 200 g situada en 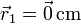 y dos de 100 g que se encuentran en
y dos de 100 g que se encuentran en 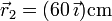 y
y 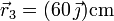 , respectivamente. Las velocidades de las masas valen cada una
, respectivamente. Las velocidades de las masas valen cada una 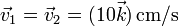 y
y 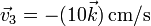
4.1 Pregunta 1
¿Cuál es la posición del centro de masas del sistema?
- A
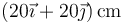 .
.
- B
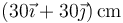 .
.
- C
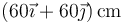 .
.
- D
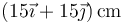 .
.
- A
4.1.1 Solución
4.2 Pregunta 2
¿Cuánto vale el momento de inercia de este sólido respecto a un eje que pasa por 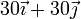 (cm) y tiene la dirección del vector
(cm) y tiene la dirección del vector  ?
?
- A 0.12 kg·m².
- B 3.60 kg·m².
- C 7.20 kg·m².
- D 1.80 kg·m².
4.2.1 Solución
4.3 Pregunta 3
Si en este sólido se aplica sobre la masa de 200 g una fuerza 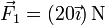 y sobre las masas
de 100 g una fuerza
y sobre las masas
de 100 g una fuerza  . ¿Cuánto vale la aceleración del centro de masas del sólido?
. ¿Cuánto vale la aceleración del centro de masas del sólido?
- A
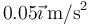 .
.
- B Es nula.
- C
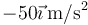 .
.
- D
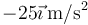 .
.
- A





