Preguntas de test de cinemática del movimiento rectilíneo (GIE)

De Laplace

Revisión a fecha de 09:34 30 oct 2013; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Identificación de movimiento
- 1.1 Solución
2 Cálculo de velocidad media
- 2.1 Solución
3 Propiedades de un m.a.s.
- 3.1 Pregunta 1
  - 3.1.1 Solución
- 3.2 Pregunta 2
  - 3.2.1 Solución
4 Movimiento con dependencia exponencial
- 4.1 Solución
5 Gráfica de una aceleración
6 Estudio de un m.a.s.

1 Identificación de movimiento

Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

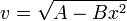
$v = \sqrt{A- B x^2}$

con $A$ y $B$ constantes positivas. La aceleración de una partícula que obedece esta ecuación es…

A proporcional a la posición x.
B nula.
C constante no nula.
D una combinación complicada de raíces cuadradas y polinomios.

1.1 Solución

La respuesta correcta es la A.

La aceleración en este movimiento vale

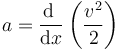
$a=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{v^2}{2}\right)$

siendo

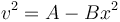
$v^2 = A - Bx^2\,$

nos queda

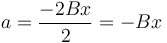
$a = \frac{-2Bx}{2}=-Bx$

Vemos que la aceleración es proporcional a la posición. Es más, se trata de un oscilador armónico.

2 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

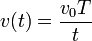
$v(t) = \frac{v_0T}{t}$

¿Cuánto vale la velocidad media entre $t = T$ y $t = 3 T$ ?

A $0.667 v 0$
B $0.500 v 0$
C $0.549 v 0$
D No hay información suficiente para determinarla.

2.1 Solución

La respuesta correcta es la C.

La velocidad media en un intervalo es igual al cociente entre el desplazamiento realizado en un intervalo y la duración de este intervalo

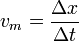
$v_m = \frac{\Delta x}{\Delta t}$

La duración del intervalo es la diferencia entre el instante inicial final y el inicial

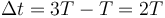
$\Delta t = 3T-T = 2T\,$

mientras que el desplazamiento es la suma de los desplazamientos infinitesimales, y por tanto igual a la integral de la velocidad instantánea

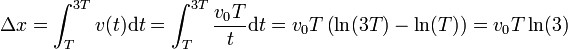
$\Delta x = \int_T^{3T} v(t)\mathrm{d}t = \int_T^{3T}\frac{v_0T}{t}\mathrm{d}t = v_0T\left(\ln(3T)-\ln(T)\right)=v_0T\ln(3)$

La velocidad media vale entonces

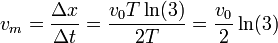
$v_m = \frac{\Delta x}{\Delta t} = \frac{v_0T\ln(3)}{2T}=\frac{v_0}{2}\ln(3)$

cuyo valor numérico es

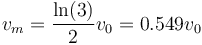
$v_m = \frac{\ln(3)}{2}v_0 = 0.549v_0$

3 Propiedades de un m.a.s.

Una partícula describe un movimiento armónico simple de frecuencia angular $ω$ , pudiéndose mover a lo largo de una recta horizontal. En $t = 0$ pasa por la posición de equilibrio con una velocidad $+ v 0$ .

3.1 Pregunta 1

¿Cuánto vale la velocidad media entre $t = 0$ y $t = T / 4$ , con $T$ el periodo de oscilación?

A $2 v 0 / π$
B Es nula.
C $v 0 / 4$
D $v 0 / 2$

3.1.1 Solución

La respuesta correcta es la A.

La velocidad media de una partícula en un movimiento rectilíneo se calcula como el cociente entre el desplazamiento neto y la duración del intervalo en que se realiza

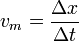
$v_m = \frac{\Delta x}{\Delta t}$

En este caso, el intervalo se nos da como dato: es la cuarta parte del periodo

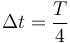
$\Delta t = \frac{T}{4}$

En un movimiento armónico simple, una partícula que parte del punto de equilibrio en $t = 0$ alcanza la máxima elongación en $T / 4$ ; en $T / 2$ vuelve a pasar por el origen en $3 T / 4$ alcanza la distancia máxima por el lado opuesto y en $T$ regresa al origen, completando el ciclo.

Por tanto el desplazamiento entre $t = 0$ y $t = T / 4$ es igual a la elongación máxima, es decir a la amplitud.

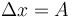
$\Delta x = A\,$

y la velocidad media será igual a

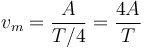
$v_m = \frac{A}{T/4} = \frac{4A}{T}$

Queda calcular la amplitud a partir de los datos del enunciado.

Tenemos que la ecuación general de un movimiento armónico simple es

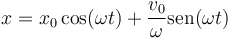
$x = x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

En esta ocasión la posición inicial es nula y el movimiento se reduce a un seno, como en la gráfica anterior

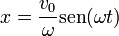
$x = \frac{v_0}{\omega}\mathrm{sen}(\omega t)$

La máxima elongación se da cuando el seno vale 1, por lo que la amplitud vale

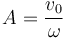
$A = \frac{v_0}{\omega}$

y queda la velocidad media

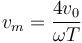
$v_m = \frac{4v_0}{\omega T}$

pero

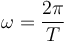
$\omega = \frac{2\pi}{T}$

lo que nos da finalmente

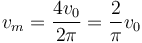
$v_m = \frac{4v_0}{2\pi} = \frac{2}{\pi}v_0$

3.2 Pregunta 2

¿Cuánto vale la aceleración en $t = T / 4$ ?

A $+ 4 v 0 / T$
B Es nula.
C $- 4 v 0 / T$
D $- v 0 ω$

3.2.1 Solución

La respuesta correcta es la D.

La aceleración en un movimiento armónico simple tiene la expresión

a = - ω 2 x

con $x$ la posición medida respecto a la de equilibrio. En $t = T / 4$ la elongación es la máxima y

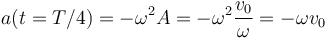
$a(t=T/4) = -\omega^2 A = -\omega^2 \frac{v_0}{\omega} = -\omega v_0$

4 Movimiento con dependencia exponencial

En un movimiento rectilíneo en el que la velocidad depende de la posición como

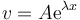
$v = A\mathrm{e}^{\lambda x}\,$

¿cuánto vale la aceleración?

A $a = 0$
B $a = A λe λ x$
C $a = A 2 λe 2λ x$
C $a = A 2 e 2λ x / 2$

4.1 Solución

La respuesta correcta es la C.

Hallamos la aceleración calculando la derivada de la velocidad respecto al tiempo, lo cual se consigue aplicando la regla de la cadena

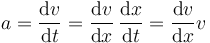
$a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}x}v$

lo que da

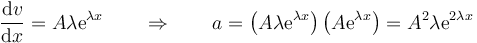
$\frac{\mathrm{d}v}{\mathrm{d}x}=A\lambda\mathrm{e}^{\lambda x}\qquad\Rightarrow\qquad a = \left(A\lambda\mathrm{e}^{\lambda x}\right)\left(A\mathrm{e}^{\lambda x}\right)=A^2\lambda\mathrm{e}^{2\lambda x}$

Alternativamente, podemos calcularlo directamente a partir de

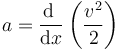
$a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{v^2}{2}\right)$

queda

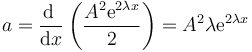
$a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{A^2\mathrm{e}^{2\lambda x}}{2}\right) = A^2\lambda\mathrm{e}^{2\lambda x}$

5 Gráfica de una aceleración

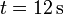La gráfica de la figura representa la aceleración de un movimiento rectilíneo entre $t = 0\,\mathrm{s}$ y $t=12\,\mathrm{s}$ . La partícula parte del reposo en $x = 0$ .

5.1 Pregunta 1=

¿Cuánto vale la rapidez en 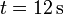$t=12\,\mathrm{s}$ ?

A 36 m/s.
B Es nula.
C 18 m/s.
D 72 m/s.

5.1.1 Solución

La respuesta correcta es la B.

La ecuación de esta aceleración es, en el SI,

$a(t) = 6-t\,$

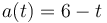
que integrada nos da la velocidad instantánea

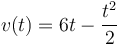
$v(t) = 6t - \frac{t^2}{2}\,$

En t = 12s esta velocidad vale

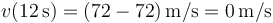
$v(12\,\mathrm{s}) =(72-72)\,\mathrm{m}/\mathrm{s}=0\,\mathrm{m}/\mathrm{s}$

con lo que la rapidez en ese instante es también nula. Gráficamente esto quiere decir que en la gráfica de la aceleración, el a´rea sobre el eje equivale al área bajo él.

5.2 Pregunta 2

¿Cuánto vale la rapidez en $t=6\,\mathrm{s}$ ?

A 36 m/s.
B Es nula.
C 18 m/s.
D 72 m/s.

5.2.1 Solución

La respuesta correcta es la C.

Para este instante, en cambio

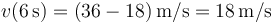
$v(6\,\mathrm{s}) = (36-18)\,\mathrm{m}/\mathrm{s}=18\,\mathrm{m}/\mathrm{s}$

que también es el valor de la rapidez en ese instante.

5.3 Pregunta 3

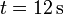¿Cuál es el desplazamiento neto entre $t=0\,\mathrm{s}$ y $t=12\,\mathrm{s}$ ?

A 72 m.
B 144 m.
C 0 m.
D -432 m.

5.3.1 Solución

La respuesta correcta es la B.

Para hallar el desplzamiento debemos integrar la velocidad, con el resultado

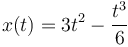
$x(t) = 3t^2 -\frac{t^3}{6}$

que en t=12s vale

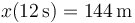
$x(12\,\mathrm{s}) = 144\,\mathrm{m}$

Puesto que la posición inicial es x=0, el desplazamiento en este intervalo es

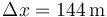
$\Delta x = 144\,\mathrm{m}$

6 Estudio de un m.a.s.

Una partícula describe un movimiento armónico simple alrededor de $x = 0$ tal que comienza en la posición de equilibrio con velocidad +0.40 m/s alcanzando el máximo alejamiento en $t=2\,\mathrm{s}$

¿Cuánto vale la amplitud del movimiento?

A 0.31 m
B No hay información suficiente para hallarla
C 0.80 m
D 0.51 m

¿Cuánto vale la aceleración cuando pasa por 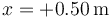$x=+0.50\,\mathrm{m}$ ?

A +0.20m/s²
B -0.31m/s²
C Es nula.
D −0.20m/s²

¿Cuánto tiempo tarda en pasar por primera vez por 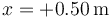$x=+0.50\,\mathrm{m}$ ?

A 1.25 s
B 1.76 s
C 0.80 s
D Nunca llega a esa posición.

Preguntas de test de cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Identificación de movimiento

1.1 Solución

2 Cálculo de velocidad media

2.1 Solución

3 Propiedades de un m.a.s.

3.1 Pregunta 1

3.1.1 Solución

3.2 Pregunta 2

3.2.1 Solución

4 Movimiento con dependencia exponencial

4.1 Solución

5 Gráfica de una aceleración

5.1 Pregunta 1=

5.1.1 Solución

5.2 Pregunta 2

5.2.1 Solución

5.3 Pregunta 3

5.3.1 Solución

6 Estudio de un m.a.s.

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES