Caso particular de dos resortes enfrentados

De Laplace

Revisión a fecha de 18:32 2 jul 2013; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Posición de equilibrio
3 Oscilaciones alrededor del equilibrio
4 Liberación del muelle 2
5 Liberación del muelle 1

1 Enunciado

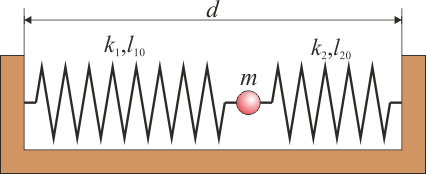
Una masa 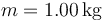$m=1.00\,\mathrm{kg}$ se encuentra atada a dos paredes separadas una distancia 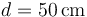$d= 50\,\mathrm{cm}$ mediante dos resortes, uno (el de la izquierda) con constante de recuperación 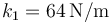$k_1=64\,\mathrm{N}/\mathrm{m}$ y longitud natural 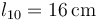$l_{10}=16\,\mathrm{cm}$ , y el otro con constante 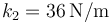$k_2=36\,\mathrm{N}/\mathrm{m}$ y longitud natural 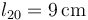$l_{20}=9\,\mathrm{cm}$ . El conjunto se encuentra sobre una superficie horizontal sin rozamiento, de forma que el peso puede ser ignorado.

Determine la distancia de la masa a las dos paredes cuando se encuentra en la posición de equilibrio. ¿Qué fuerza ejerce cada muelle sobre la masa?
Si estando en la posición de equilibrio se comunica una velocidad de 0.20 m/s a la masa hacia la derecha, ¿cuál es la amplitud de las oscilaciones que describe? ¿Y su frecuencia angular ω?
Suponga de nuevo que la masa se encuentra en reposo en la posición de equilibrio y bruscamente se corta su unión con el muelle 2. ¿Que amplitud tienen las oscilaciones de la masa y qué frecuencia angular?
Si en el apartado anterior, el muelle que se corta es el 1, manteniéndose la unión con el 2, ¿se producen oscilaciones? ¿Con qué amplitud y frecuencia natural?

2 Posición de equilibrio

Este problema es en gran medida una repetición del problema “Dos resortes enfrentados”, aunque por completitud, repetiremos aquí los cálculos que se allí se hacen.

La partícula está sometida a dos fuerzas elásticas. Al ser ambas horizontales, podemos hacer el cálculo en una dimensión y precidin de vectores. No obstante habrá que tener cuidado con los signos, ya que estos determinan el sentido de la fuerza. Positivo implica hacia la derecha y negativo hacia la izquierda.

Sea $x$ la distancia a la pared de la izquierda. La fuerza elástica debida al muelle de la izquierda es

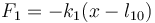
$F_1 =-k_1(x-l_{10})\,$

El signo lo da el que si $x$ es mayor que $l 10$ el muelle se estira. Al producirse una fuerza recuperadora, esta va hacia la izquierda, por lo que es negativa.

Para el muelle de la derecha, la distancia a la pared correspondiente es $d - x$ , por lo que la fuerza debida a este muelle vale

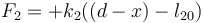
$F_2 = +k_2((d-x)-l_{20})\,$

El signo positivo no se debe a que haya cambiado la ley de Hooke, sino que si la longitud de este muelle es mayor que la longitud natural ( $(d - x) > l 20$ ), la fuerza recuperadora va hacia la derecha, es decir, es positiva.

En la posición de equilibrio, la suma de fuerzas se anula

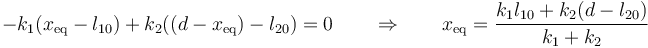
$-k_1(x_\mathrm{eq}-l_{10})+k_2((d-x_\mathrm{eq})-l_{20})=0\qquad \Rightarrow\qquad x_\mathrm{eq} = \frac{k_1l_{10}+k_2(d-l_{20})}{k_1+k_2}$

siendo su valor numérico

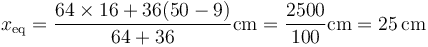
$x_\mathrm{eq} = \frac{64\times 16 + 36(50-9)}{64+36}\mathrm{cm}=\frac{2500}{100}\mathrm{cm}=25\,\mathrm{cm}$

Puesto que la distancia entre paredes es de 50cm, la masa se halla en el punto medio y las dos distancias son iguales

$d_1 = x_\mathrm{eq}=25\mathrm{cm}\qquad\qquad d_2=d-x_\mathrm{eq}=25\,\mathrm{cm}$

La fuerza que cada resorte ejerce sobre la masa la obtenemos de las expresiones anteriores de la ley de Hooke, pasando las distancias al SI

$F_1 = -64(0.25-0.16)\mathrm{N}=-5.76\,\mathrm{N}\qquad\qquad F_2 =+36(0.25-0.09)\,\mathrm{N}=+5.76\,\mathrm{N}$

Las dos fuerzas son iguales y opuestas, como corresponde a que la masa se encuentre en equilibrio.

3 Oscilaciones alrededor del equilibrio

Si la partícula se encuentra en una posición que no sea la de equilibrio, o moviéndose, o ambas cosas, ya la situación no será de reposo, sino que se mueve gobernada por la segunda ley de Newton. En una dimensión

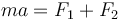
$ma = F_1 + F_2\,$

Sustituyendo las fuerzas elásticas queda

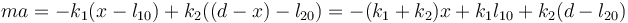
$ma = -k_1(x-l_{10})+k_2((d-x)-l_{20}) = -(k_1+k_2)x + k_1 l_{10}+k_2(d-l_{20})\,$

Los dos últimos términos son sproporcionales a la distancia de equilibrio, por lo que la ley de Newton se reduce a

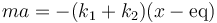
$ma = -(k_1+k_2)(x-\mathrm{eq})\,$

Esta ecuación nos dice que el comportamiento del sistema es el de un oscilador armónico de constante equivalente

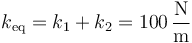
$k_\mathrm{eq}=k_1+k_2=100\,\frac{\mathrm{N}}{\mathrm{m}}$

siendo la frecuencia de oscilación

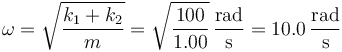
$\omega=\sqrt{\frac{k_1+k_2}{m}}=\sqrt{\frac{100}{1.00}}\,\frac{\mathrm{rad}}{\mathrm{s}} = 10.0\,\frac{\mathrm{rad}}{\mathrm{s}}$

La amplitud de las oscilaciones la podemos hallar a partir de la fórmula

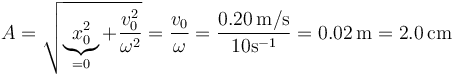
$A=\sqrt{\underbrace{x_0^2}_{=0}+\frac{v_0^2}{\omega^2}}=\frac{v_0}{\omega}=\frac{0.20\,\mathrm{m}/\mathrm{s}}{10 \mathrm{s}^{-1}}=0.02\,\mathrm{m}=2.0\,\mathrm{cm}$

o bien por la ley de conservación de la energía

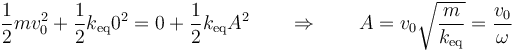
$\frac{1}{2}mv_0^2 + \frac{1}{2}k_\mathrm{eq}0^2=0+\frac{1}{2}k_\mathrm{eq}A^2 \qquad\Rightarrow\qquad A = v_0\sqrt{\frac{m}{k_\mathrm{eq}}}=\frac{v_0}{\omega}$

4 Liberación del muelle 2

Volviendo a la posición de reposo, tenemos la masa estacionaria en 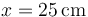$x=25\,\mathrm{cm}$ .

Si ahora cortamos el muelle 2, la masa pasa a estar sometida a la fuerza elástica del muelle 1,

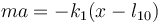
$ma = -k_1(x-l_{10})\,$

Esta es también la ecuación de un oscilador armónico, pero de constante $k 1$ , y con una posición de equilibrio dada por la longitud natural de este resorte, 16cm. Puesto que la masa no se halla en este punto, comenará a oscilar en torno a esta nueva posición de equilibrio. La nueva frecuencia de oscilación es

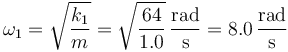
$\omega_1 = \sqrt{\frac{k_1}{m}}=\sqrt{\frac{64}{1.0}}\,\frac{\mathrm{rad}}{\mathrm{s}}=8.0\,\frac{\mathrm{rad}}{\mathrm{s}}$

y puesto que parte del reposo, la amplitud será igual a la distancia entre la posición inicial y la nueva posición de equilibrio

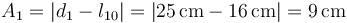
$A_1 = |d_1-l_{10}| = |25\,\mathrm{cm}-16\,\mathrm{cm}| = 9\,\mathrm{cm}$

La masa oscilará llegando a quedarse a solo 7 cm de la pared.

5 Liberación del muelle 1

En el segundo caso, el análisis sería similar, siendo ahora las oscilaciones en torno a la posición de equilibrio del muelle 2. La nueva frecuencia de oscilación sería

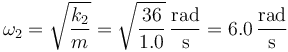
$\omega_2 = \sqrt{\frac{k_2}{m}}=\sqrt{\frac{36}{1.0}}\,\frac{\mathrm{rad}}{\mathrm{s}}=6.0\,\frac{\mathrm{rad}}{\mathrm{s}}$

y la nueva amplitud

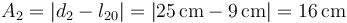
$A_2 = |d_2-l_{20}| = |25\,\mathrm{cm}-9\,\mathrm{cm}| = 16\,\mathrm{cm}$

Pero, ¿qué ocurre? Que esta amplitud es mayor que la propia longitud natural del muelle. Esto quiere decir que la masa llegaría a golpear la pared, o bien, lo que es más realista, que el muelle se comprimiría tanto que dejaría de cumplir la ley de Hooke.

Esto quiere decir que en este caso no se producen oscilaciones armónicas. Tanto si choca, como si simplemente se deforma el muelle, ya deja de cumplirse la ley de Hooke.

Caso particular de dos resortes enfrentados

De Laplace

Contenido

1 Enunciado

2 Posición de equilibrio

3 Oscilaciones alrededor del equilibrio

4 Liberación del muelle 2

5 Liberación del muelle 1

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES