Entrar Página Discusión Historial Go to the site toolbox

Esfera que se conecta a una fuente de tensión

De Laplace

Contenido

1 Enunciado

Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga 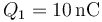Q_1=10\,\mathrm{nC}. Alrededor de la esfera no hay más conductores ni cargas.

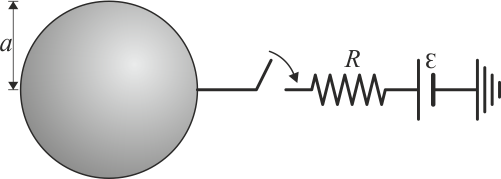
Archivo:esfera-fuente.png
  1. Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
  2. Suponga que ahora se conecta a la esfera una fuente de tensión de 3.0 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
  3. Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
  4. ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
  5. Determine la ecuación diferencial que gobierna el potencial V(t) de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de V(t) frente al tiempo.

Dato: 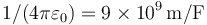1/(4\pi\varepsilon_0) = 9\times 10^9\,\mathrm{m}/\mathrm{F}

2 Estado inicial de la esfera

Cuando tenemos una esfera conductora de radio a que almacena una carga Q, el potencial de su superficie (y del interior también) es

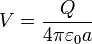
V = \frac{Q}{4\pi\varepsilon_0a}

así que en este caso el potencial inicial de la esfera vale

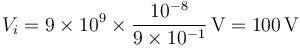
V_i = 9\times 10^9\times\frac{10^{-8}}{9\times 10^{-1}}\,\mathrm{V}=100\,\mathrm{V}

y la energía almacenada en el sistema es

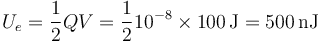
U_e = \frac{1}{2}QV = \frac{1}{2}10^{-8}\times 100\,\mathrm{J}=500\,\mathrm{nJ}

3 Corriente eléctrica

Una vez que se conecta la fuente, aparece una d.d.p. entre los extremos de la resistencia. Por un lado tenemos la esfera a 100 V y por otro la fuente a 3000 V. La intensidad de corriente que circula por la resistencia en ese instante inicial es

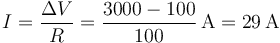
I = \frac{\Delta V}{R}=\frac{3000-100}{100}\,\mathrm{A}=29\,\mathrm{A}

Nótese que es I = ΔV / R, no I = V / R.

Esta corriente va de mayor a menor voltaje, por tanto va hacia la esfera, y la carga de esta irá aumentando.


4 Estado final

5 Balance energético

6 Evolución del voltaje

Obtenido de "http://tesla.us.es/wiki/index.php/Esfera_que_se_conecta_a_una_fuente_de_tensi%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace