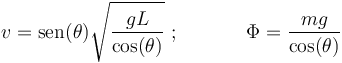No Boletín - Péndulo cónico (Ex.Ene/13)
De Laplace
1 Enunciado
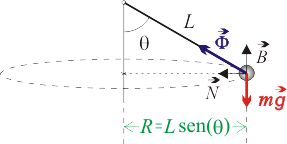
Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es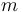 
, la longitud del péndulo es 
, el ángulo que forma el hilo con la vertical es 
y la gravedad es 
.
- ¿Con qué celeridad se mueve la masa puntual?
- ¿Cuál es el módulo de la tensión del hilo?
2 Solución
La masa puntual describe con celeridad constante 
(movimiento uniforme) una circunferencia de radio:
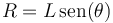
y lo hace bajo la acción de dos fuerzas: el peso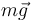 
y la tensión ejercida por el hilo 
.
Para expresar las magnitudes vectoriales del ejercicio, utilizaremos el triedro intrínseco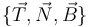 
de la circunferencia (en la figura adjunta se omite el vector tangente 
).
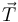El peso es una fuerza activa y, como tal, totalmente conocida a priori:
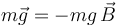
Sin embargo, la tensión del hilo es una fuerza de reacción vincular, de módulo 
en principio desconocido, con dirección a lo largo del hilo y sentido hacia el punto de suspensión del hilo:
![\vec{\Phi}=\Phi[\mathrm{sen}(\theta)\,\vec{N}+\mathrm{cos}(\theta)\,\vec{B}]](/wiki/images/math/f/a/6/fa6938662c1a261c7a1e9de1d159c94d.png)
Dado que la masa puntual describe un movimiento circular uniforme, sabemos que su aceleración sólo va a tener componente normal:
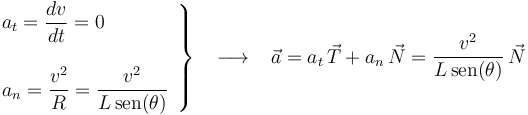
Aplicando la segunda ley de Newton, y separando componentes, se llega al siguiente sistema de ecuaciones (para las incógnitas y ):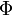
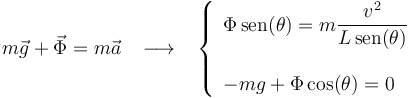
Resolviéndolo, obtenemos los valores de la celeridad de la partícula, y del módulo 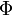de la tensión del hilo:
