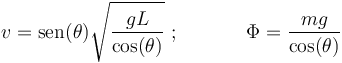No Boletín - Péndulo cónico (Ex.Ene/13)
De Laplace
1 Enunciado
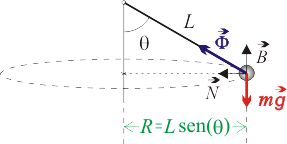
Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es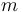 
, la longitud del péndulo es 
, el ángulo que forma el hilo con la vertical es 
y la gravedad es 
.
- ¿Con qué celeridad se mueve la masa puntual?
- ¿Cuál es el módulo de la tensión del hilo?
2 Solución
La masa puntual describe con celeridad constante 
(movimiento uniforme) una circunferencia de radio:
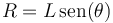
y lo hace bajo la acción de dos fuerzas: el peso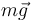 
y la tensión ejercida por el hilo 
.
Para expresar las magnitudes vectoriales, utilizaremos el triedro intrínseco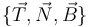 
de la circunferencia.
El peso es una fuerza activa y, como tal, es conocida a priori:
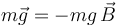
Sin embargo, la tensión del hilo es una fuerza de reacción vincular, de módulo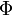 
en principio desconocido, con dirección a lo largo del hilo y sentido hacia el punto de suspensión del hilo:
![\vec{\Phi}=\Phi[\,\mathrm{sen}(\theta)\,\vec{N}+\mathrm{cos}(\theta)\,\vec{B}\,]](/wiki/images/math/c/c/7/cc7b21a1b7dc0d599c0f60bf82eae40b.png)
Dado que la masa puntual describe un movimiento circular uniforme, sabemos que su aceleración sólo va a tener componente normal:
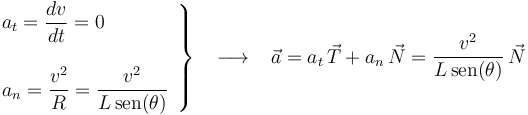
Aplicando la segunda ley de Newton, y separando componentes, se llega al siguiente sistema de ecuaciones (para las incógnitas y ):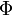
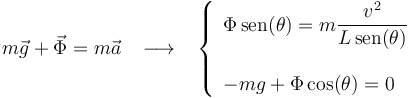
Resolviendo el sistema, obtenemos los valores de la celeridad de la partícula y del módulo 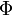de la tensión del hilo:
