No Boletín - Cálculo de una diagonal (Ex.Ene/13)
De Laplace
Revisión a fecha de 12:01 27 feb 2013; Enrique (Discusión | contribuciones)
1 Enunciado
Sea el rombo cuyos lados quedan definidos por los vectores 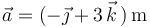 y
y
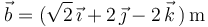 . ¿Cuál es la longitud de su diagonal mayor?
. ¿Cuál es la longitud de su diagonal mayor?
2 Solución
Si 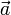 y
y 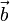 definen los lados de un rombo, es trivial comprobar (por la definición geométrica de la suma y de la diferencia de vectores) que las diagonales del rombo vienen dadas por los vectores
definen los lados de un rombo, es trivial comprobar (por la definición geométrica de la suma y de la diferencia de vectores) que las diagonales del rombo vienen dadas por los vectores 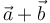 y
y 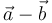 :
:

Las longitudes de las diagonales se calculan tomando módulos:

Y comparando las longitudes, comprobamos que la diagonal mayor es la que mide 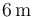 .
.





