Clasificación de movimientos de un sólido
De Laplace
Revisión a fecha de 12:39 13 ene 2013; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Se tiene un sólido formado por ocho masas iguales, 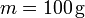 , situadas en los vértices de un cubo de lado
, situadas en los vértices de un cubo de lado 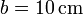 . En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
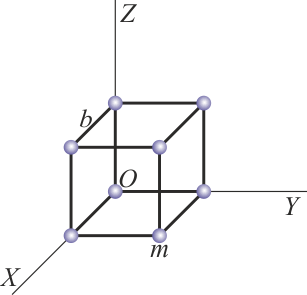
Considere los casos siguientes para las velocidades de las masas situadas en 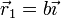 ,
, 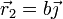 y
y 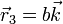
| Caso | 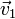 (cm/s) (cm/s)
| 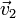 (cm/s) (cm/s)
| 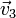 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 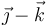
| 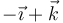
| 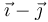
|
| II | 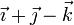
| 
| 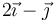
|
| III | 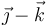
| 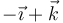
| 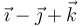
|
| IV | 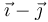
| 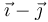
| 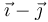
|
| V | 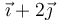
| 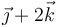
| 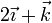
|
| VI | 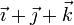
| 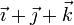
| 
|
- Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
- Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
- Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
2 Introducción
Para cada uno de los casos, el procedimiento es el siguiente:
- Se comprueba si verifican la condición cinemática de rigidez, de forma que para cada par de puntos
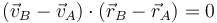
- Si no se cumple, ya hemos acabado.
- Si mira si las velocidades de los tres puntos son iguales. Si lo son, el movimiento es una traslación con dicha velocidad. En particular, si hay tres puntos no alineados con velocidad nula, el estado es de reposo.
- Si no ocurre lo anterior, pero uno de los puntos tiene velocidad nula, el movimiento es una rotación alrededor de un eje que pasa por este punto. La velocidad angular se saca de la velocidad de los otros puntos.
- Si dos puntos tienen la misma velocidad y el tercero no, el EIRMD (o EIR en su caso) apunta en la dirección de la recta que pasa por los dos puntos. De aquí se saca la velocidad de deslizamiento y de la velocidad del tercer punto la velocidad angular.
- Si no se aplica nada de lo anterior, hay que recurrir a la expresión del teorema de Chasles
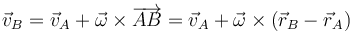
- para hallar el vector ω.
- El EIR o EIRMD, si no se ha localizado previamente, se determina empleando la fórmula
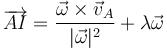
- que nos da la posición de los puntos del eje respecto al punto A.
3 Caso I
Comprobamos la condición cinemática de rigidez. Tenemos que, midiendo las distancias en cm y las velocidades en cm/s