Momento de inercia de un sólido en L
De Laplace
1 Enunciado
Se tiene un sólido en forma de L de un metal homogéneo, siendo h la longitud de los brazos y M su masa total. Calcule el momento de inercia del sólido respecto a un eje perpendicular al plano de la L y que pasa por un punto del interior del cuadrado de lado h que define. ¿En qué punto es mínimo este momento de inercia?
2 Momento de inercia general
Para hallar el momento de inercia del sólido completo, lo consideramos como compuesto de dos varillas, cuyos momentos hallamos por separado, de forma que
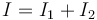
Para hallar el momento de inercia de la varilla “1” respecto a un punto cualquiera aplicamos el teorema de Steiner
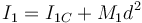
siendo I1C el momento de inercia de la varilla respecto a un eje paralelo pero que pasa por su centro de masas y d la distancia entre el eje original y el paralelo.
En este caso, estamos considerando un eje perpendicular a la varilla, por lo que el momento respecto a su centro de masas es
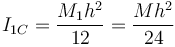
donde hemos aplicado que M1 = M / 2





