Masa arrastrada sobre una mesa

De Laplace

1 Enunciado

Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.

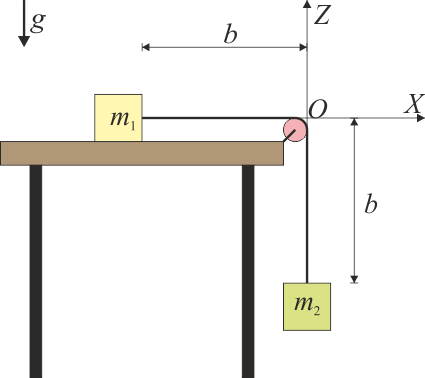
Empleando el sistema de ejes de la figura y para el instante reflejado en ella:

1. ¿Cuál es la aceleración de cada una de las masas?
2. ¿Dónde se halla el centro de masas?
3. ¿Cuál es la aceleración del CM?
4. Si en el isntante representado la masa 1 tiene una rapidez v₀, ¿cuánto vale la velocidad del CM?
5. Para el caso de apartado anterior, ¿cuánto valen la cantidad de movimiento, la energía cinética y el momento cinético respecto al origen y respecto al CM?

2 Aceleraciones

Este sistema es un caso particular de otro estudiado en un problema de dinámica. Para calcular las aceleraciones respectivas realizamos los diagramas de cuerpo libre, considerando cada masa por separado, incluyendo todas las fuerzas que actúan sobre ellas.

Sobre la masa 1 actúan tres fuerzas: su peso, la reacción normal de la mesa y la tensión de la cuerda que tira de ella. Si hubiera rozamiento también deberíamos incluirlo, pero no es el caso. Por tanto tenemos

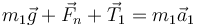
Para la segunda masa las únicas fuerzas que actúan son su peso y la tensión que tiera de ella hacia arriba

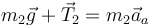
Separando en componentes cada una de estas ecuaciones tenemos, para la primera masa

ya que su aceleración es puramente horizontal. Para la segunda masa obtenemos una sola ecuación escalar

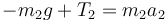
Por tratarse de un hilo ideal sin masa, el módulo de la tensión en el extremo de la masa 1 es igual al del otro extremo

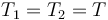
y por ser inextensible la rapidez y la aceleración horizontal de la masa 1 debe coincidir con la de la masa 2,

El signo negativo proviene de que, de acuerdo con el sistema de ejes elegido hemos considerado

es decir, ambas dirigidas hacia la polea, por lo que una de ellas debe ser negativa.

Con estas simplificaciones queda el sistema

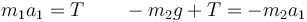
Sumando las dos ecuaciones hallamos las aceleraciones

y, en forma vectorial,

En el caso particular m₁ = m₂ = m

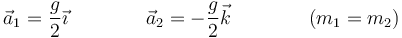
3 Posición del CM

El centro de masas es la media ponderada de las posiciones respectivas

para la posición de la figura

resulta la posición del CM

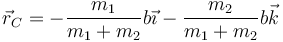
Este punto se halla sobre la recta que une las dos partículas (o, para ser precisos, sus respectivos centros de masas). Si además las dos masas son iguales, el centro de masas se halla en el punto medio entre ellas

4 Aceleración del CM

De manera análoga hallamos la aceleración del centro de masas

que en este caso nos da

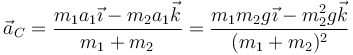
si además las masas son iguales

5 Velocidad del CM

6 Propiedades del sistema

6.1 Cantidad de movimiento

6.2 Energía cinética

6.3 Momento cinético