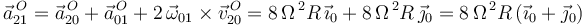No Boletín - Disco en barra ranurada (Ex.Ene/12)
De Laplace
Contenido |
1 Enunciado
Mediante un par de revolución, la barra ranurada horizontal 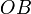 (sólido "0") gira en el sentido indicado en la figura con velocidad angular de módulo constante
(sólido "0") gira en el sentido indicado en la figura con velocidad angular de módulo constante 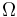 alrededor del eje vertical
alrededor del eje vertical 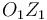 del triedro fijo
del triedro fijo 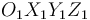 (sólido "1"). A su vez, un disco (sólido "2") de radio
(sólido "1"). A su vez, un disco (sólido "2") de radio  , contenido en todo instante en el plano vertical
, contenido en todo instante en el plano vertical 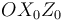 , rota en el sentido indicado en la figura con velocidad angular de módulo constante
, rota en el sentido indicado en la figura con velocidad angular de módulo constante 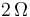 , mientras que su centro
, mientras que su centro  se desplaza por la ranura de la barra con celeridad constante
se desplaza por la ranura de la barra con celeridad constante 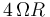 en el sentido positivo del eje
en el sentido positivo del eje 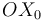 . En el instante representado en la figura, y al
que se refieren las siguientes preguntas, el centro
. En el instante representado en la figura, y al
que se refieren las siguientes preguntas, el centro  del disco se halla a distancia
del disco se halla a distancia  del extremo
del extremo  de la barra, y se denomina
de la barra, y se denomina  al punto del disco que ocupa la posición más alta.
al punto del disco que ocupa la posición más alta.
- Determine la posición del EIR{20}
- Calcule la velocidad instantánea
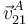
- Calcule la aceleración instantánea
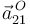
2 Datos del problema
Comenzamos expresando en la base vectorial 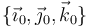 , asociada al triedro
, asociada al triedro 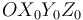 , los datos que se deducen del enunciado:
, los datos que se deducen del enunciado:
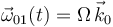 ;
; 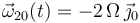 ;
; 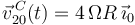 ;
; 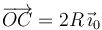 ;
; 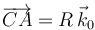
3 Posición del EIR{20}
Sabemos que el EIR{20} tiene la dirección de 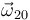 . Por tanto, se trata de una recta paralela al eje
. Por tanto, se trata de una recta paralela al eje 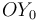 (perpendicular al plano
(perpendicular al plano 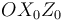 ). Para calcular un punto
). Para calcular un punto 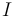 que pertenezca al eje EIR{20}, utilizamos la fórmula habitual:
que pertenezca al eje EIR{20}, utilizamos la fórmula habitual:
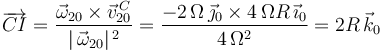
NOTA: Este ejercicio se puso en un examen tipo test, en el cual la respuesta correcta para definir la posición del punto 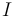 por el que pasa el EIR{20} era:
por el que pasa el EIR{20} era: 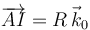 , que evidentemente es equivalente a
, que evidentemente es equivalente a 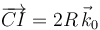 dado que
dado que 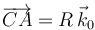 .
.
En definitiva, las ecuaciones del EIR{20} en el triedro 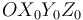 son:
son:
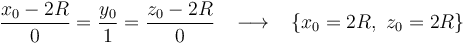
4 Velocidad instantánea del punto A en el movimiento {21}
Empezamos calculando la velocidad relativa del punto  (
(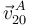 ) a partir de la velocidad relativa del punto
) a partir de la velocidad relativa del punto  (
(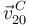 ) mediante la ecuación del campo de velocidades del movimiento {20}:
) mediante la ecuación del campo de velocidades del movimiento {20}:
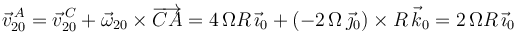
A continuación, calculamos la velocidad de arrastre del punto  (
(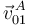 ) a partir de la velocidad de arrastre del punto
) a partir de la velocidad de arrastre del punto  (
(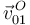 ) mediante la ecuación del campo de velocidades del movimiento {01}:
) mediante la ecuación del campo de velocidades del movimiento {01}:

donde se ha tenido en cuenta que el punto  pertenece al eje permanente de rotación del movimiento {01}, es decir, se trata de un punto fijo en dicho movimiento y, por tanto,
pertenece al eje permanente de rotación del movimiento {01}, es decir, se trata de un punto fijo en dicho movimiento y, por tanto, 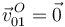 (y también
(y también 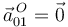 , tal como utilizaremos después).
, tal como utilizaremos después).
Finalmente, la ley de composición de velocidades nos permite determinar la velocidad absoluta del punto  (
(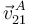 ):
):
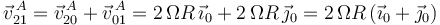
5 Aceleración instantánea del punto O en el movimiento {21}
Hallamos primero la aceleración relativa del punto  (
(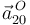 ) a partir de la aceleración relativa del punto
) a partir de la aceleración relativa del punto  (
(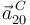 ) mediante la ecuación del campo de aceleraciones del movimiento {20}:
) mediante la ecuación del campo de aceleraciones del movimiento {20}:
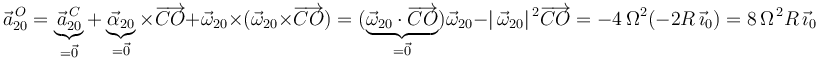
donde se ha tenido en cuenta que:
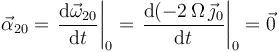
Por otra parte, tal como se adelantó antes, la aceleración de arrastre del punto  (
(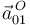 ) es nula:
) es nula:
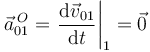
Calculamos ahora el término de aceleración de Coriolis del punto  :
:
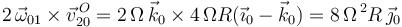
donde se ha introducido el valor de 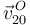 que se obtiene de:
que se obtiene de:
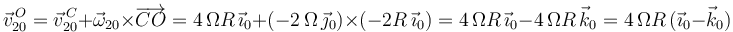
Por último, calculamos la aceleración absoluta del punto  (
(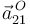 ) sumando las aceleraciones relativa, de arrastre y de Coriolis (ley de composición de aceleraciones):
) sumando las aceleraciones relativa, de arrastre y de Coriolis (ley de composición de aceleraciones):