5.5. Composición de dos rotaciones que se cruzan (Ex.Sep/12)
De Laplace
1 Enunciado
Sean tres sólidos rígidos ("0", "1" y "2") tales que el movimiento relativo {20} es una rotación alrededor del eje { 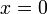 ,
, 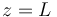 } (con
} (con 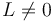 ); mientras que el movimiento de arrastre {01} es una rotación alrededor del eje {
); mientras que el movimiento de arrastre {01} es una rotación alrededor del eje { 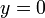 ,
, 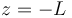 }. Las velocidades angulares relativa y de arrastre tienen ambas el mismo
módulo:
}. Las velocidades angulares relativa y de arrastre tienen ambas el mismo
módulo: 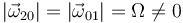 , y cada una de ellas apunta en el sentido positivo del eje cartesiano al cual es paralela.
, y cada una de ellas apunta en el sentido positivo del eje cartesiano al cual es paralela.
- ¿Qué tipo de movimiento es el absoluto {21}?
- ¿Cuál es el EIR (o EIRMD) de dicho movimiento {21}?
2 Solución
Tenemos la información necesaria para determinar los vectores 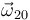 y
y 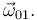 El enunciado nos proporciona sus módulos
El enunciado nos proporciona sus módulos 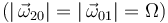 , sus direcciones
, sus direcciones 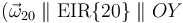 ; y
; y 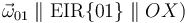 y sus correspondientes sentidos
y sus correspondientes sentidos
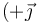 y
y 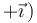 . Así que:
. Así que:

La ley de composición de velocidades angulares nos permite determinar la velocidad angular del movimiento {21}:
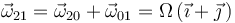
Por otra parte, observando las ecuaciones del EIR{20} y del EIR{01}, nos damos cuenta de que ambos ejes no son concurrentes, sino que se cruzan en el espacio.
NOTA: Cuando se componen dos rotaciones puras de ejes conocidos, es interesante comprobar si ambos ejes son o no concurrentes. Porque en el caso de que ambos ejes se corten en un punto, automáticamente sabemos que en dicho punto la velocidad del movimiento compuesto va a ser nula, y por tanto el movimiento compuesto será otra rotación pura cuyo eje pasará por el punto de concurrencia.
Para clasificar el movimiento {21} necesitamos ahora calcular la velocidad {21} de algún punto (para determinar después el segundo invariante). Vamos a hallar, por ejemplo, la velocidad {21} del origen de coordenadas 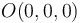 como suma de las velocidades {20} y {01} de dicho punto (ley de composición de velocidades). Y para calcular las velocidades {20} y {01} de
como suma de las velocidades {20} y {01} de dicho punto (ley de composición de velocidades). Y para calcular las velocidades {20} y {01} de  nos apoyaremos, respectivamente, en los puntos
nos apoyaremos, respectivamente, en los puntos 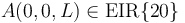 y
y 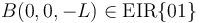 . Así:
. Así:
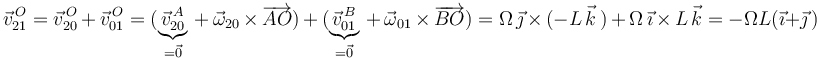
Calculamos ahora el segundo invariante:

Concluimos, pues, que el movimiento {21} es un movimiento helicoidal, ya que tanto el primer como el segundo invariante son no nulos:
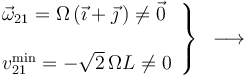 {21} es un MOVIMIENTO HELICOIDAL
{21} es un MOVIMIENTO HELICOIDAL
Obsérvese que la velocidad 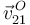 ha resultado ser paralela a la velocidad angular
ha resultado ser paralela a la velocidad angular 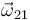 . Por tanto, el EIRMD{21} pasa por el origen de coordenadas
. Por tanto, el EIRMD{21} pasa por el origen de coordenadas  y su dirección es la dirección del vector velocidad angular del movimiento {21}. Po tanto, las ecuaciones del EIRMD{21} son:
y su dirección es la dirección del vector velocidad angular del movimiento {21}. Po tanto, las ecuaciones del EIRMD{21} son:
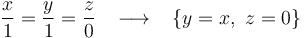
Si inicialmente no nos hubiésemos dado cuenta de que 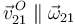 y que, por tanto,
y que, por tanto,  EIRMD{21}, lo detectaríamos al tratar de calcular un punto
EIRMD{21}, lo detectaríamos al tratar de calcular un punto 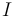 perteneciente al EIRMD{21} utilizando la fórmula habitual:
perteneciente al EIRMD{21} utilizando la fórmula habitual:






