Fuerza entre dos hilos cargados
De Laplace
Contenido |
1 Enunciado
Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga λ y − λ, situadas a una distancia D una de la otra.
Se trata de hallar la fuerza por unidad de longitud con que se atraen los dos hilos. Para ello, calcule:
- El campo eléctrico en cualquier punto del espacio, creado por un segmento rectilíneo de longitud L, sobre el cual existe una densidad de carga uniforme λ.
- A partir del resultado anterior, halle el campo en cualquier punto debido a una línea de carga uniforme infinitamente larga.
- Halle la fuerza que uno de los hilos produce sobre un segmento de longitud h del otro hilo.
2 Solución
2.1 Campo de un segmenthttp://laplace.us.es/wiki/skins/common/images/button_math.pngo cargado
Sin pérdida de generalidad, podemos colocar el eje z sobre el segmento y el origen de coordenadas en su punto medio.
La expresión integral para el campo eléctrico debido a una distribución de carga lineal se expresa
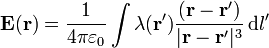
En nuestro caso, la posición de las fuentes es

![z'\in\left[-\frac{L}{2},\frac{L}{2}\right]](/wiki/images/math/b/8/c/b8c49aa8076cf8849ff4819712f2715e.png)
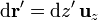
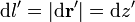
por lo que la integral se convierte en

Separando componente a componente
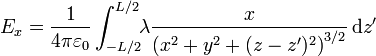
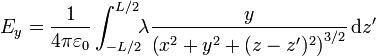
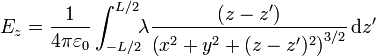
Podemos llevar a cabo estas integrales mediante el cambio de variable
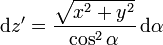
Este ángulo posee interpretación geométrica ya que es el que forma la dirección al punto donde está la fuente con la horizontal.
Con este cambio las integrales quedan
Los senos y cosenos que aparecen en las expresiones anteriores corresponden a los valores límite de α y su relación con las coordenadas cartesianas es
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \sen\alpha_2=\frac{L/2-z}{\sqrt{x^2+y^2+(z-L/2)^2}}
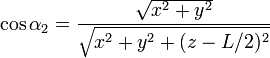
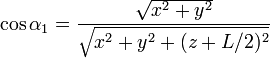
Agrupando los resultados tenemos la forma vectorial
Si expresamos el campo en coordenadas cilíndricas centradas en el hilo nos queda
que podemos leer como el campo posee una componente en la dirección radial perpendicular al eje del segmento y una componente paralela a él. Esta interpretación nos seguirá valiendo cuando el eje z no esté situado sobre el segmento.
Para ello consideraremos un segmento AB y un punto de observación arbitrario P. Trazamos la recta perpendicular a AB por P. Esta recta cortará a la primera en un punto C. La variable ρ será la longitud del segmento PC. El ángulo α1 será el que forma esta perpendicular con el segmento PA y el α2 con el segmento PB. Ambos ángulos serán positivos si la perpendicular queda por detrás del segmento (considerando adelante aquél en que apunta  ) y negativos en caso contrario. Si la perpendicular incide sobre el segmento AB, el ángulo α2 será positivo y el α1 negativo.
) y negativos en caso contrario. Si la perpendicular incide sobre el segmento AB, el ángulo α2 será positivo y el α1 negativo.
Un límite interesante de la expresión anterior es aquel en que 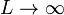 , entonces, cualquiera que sea el punto de observación,
, entonces, cualquiera que sea el punto de observación, 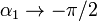 ,
, 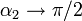 , por lo que
, por lo que
Este resultado se obtiene, empleando la ley de Gauss, en otro problema.





