Frenado de un fórmula 1

De Laplace

1 Enunciado

Cuando el Ferrari de Fernando Alonso se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 340 km/h. Cuando entra en la chicane va a 80 km/h.

1. Suponiendo que la aceleración es constante, determine su valor.
2. Exprese el resultado en el SI y como un múltiplo de g (siendo ).
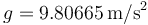3. Determine la velocidad como función de la posición y represéntela gráficamente.

2 Aceleración en el SI

Pasamos en primer lugar los valores de la velocidad al SI. A 150m de la chicane tiene una velocidad de

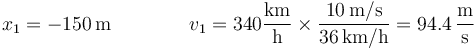
y al entrar en la chicane

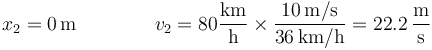
Para hallar la aceleración aplicamos que en un movimiento uniformemente acelerado

En este caso no conocemos lo que tarda en llegar a la chicane, pero no es necesario. tenemos dos ecuaciones y dos incógnitas (la aceleración y el intervalo de frenado).

Si contamos como instante inicial el del comienzo de la frenada, ya tenemos x₀ y v₀. Para el final de la frenada nos queda

x_2 = x_1 + v_1 t + \frac{1}{2}at^2 \qquad v_2 = v_1 + a t

3 “Fuerzas G”

4 Velocidad como función de la posición