Determinación de un vector a partir de sus proyecciones
De Laplace
1 Enunciado
Se tiene un vector conocido, no nulo,  y uno que se desea determinar,
y uno que se desea determinar, 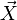 . Se dan como datos su producto escalar y su
producto vectorial por
. Se dan como datos su producto escalar y su
producto vectorial por 

Determine el valor de 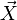 . ¿Es suficiente una sola de las dos ecuaciones para hallar
. ¿Es suficiente una sola de las dos ecuaciones para hallar 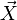 ?
?
2 Solución
Ante este problema existe la tentación de “pasar uno de los vectores al otro lado dividiendo”. Algo así como

Esta expresión no posee significado alguno, ya que no está definida la división por un vector.
La forma de hallar el vector incógnita es con ayuda del doble producto vectorial

Sustituyendo en esta expresión lo que conocemos

y de aquí sí podemos despejar 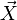 , por estar multiplicado por un escalar
, por estar multiplicado por un escalar
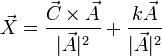
Vemos que para llegar al resultado necesitamos los dos productos, el escalar y el vectorial y no nos basta uno de ellos.
3 Interpretación geométrica
Este resultado posee una interpretación geométrica sencilla. El vector 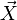 tendrá una componente paralela y una ortogonal al vector
tendrá una componente paralela y una ortogonal al vector  .
.
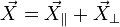
La parte paralela tendrá por módulo la proyección paralela a  y su dirección estará dada por la del unitario en la dirección de
y su dirección estará dada por la del unitario en la dirección de 

esto es, el conocimiento del producto escalar nos da la parte paralela, pero no todo el vector.
La parte perpendicular la obtenemos a partir de  , ya que
, ya que
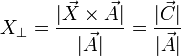
Por ello el conocimiento de solo el producto vectorial tampoco nos da todo el vector, ya que nos faltaría la parte paralela.





